湖南省怀化市洪江市2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-12-18 类型:期末考试
一、单选题
-
1. 下列方程组中,属于二元一次方程组的是( )A、 B、 C、 D、2. 下列分解因式正确的是( )A、 B、 C、 D、3. 下列是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、a•a2=a2 B、(x3)2=x5 C、(2a)2=4a2 D、(x+1)2=x2+15. 三条共点直线都与第四条直线相交,一共有( )对对顶角.A、12 B、24 C、7 D、116. 下列说法错误的是( )A、平移不改变图形的形状和大小 B、对顶角相等 C、两个直角一定互补 D、同位角相等7. 我市某中学举办了一次以“阳光少年,我们是好伙伴”为主题的演讲比赛,有9名同学参加了决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差8. 下列各数能整除 的是( )A、62 B、63 C、64 D、669. 如图, ,则 和 的关系是( )
4. 下列计算正确的是( )A、a•a2=a2 B、(x3)2=x5 C、(2a)2=4a2 D、(x+1)2=x2+15. 三条共点直线都与第四条直线相交,一共有( )对对顶角.A、12 B、24 C、7 D、116. 下列说法错误的是( )A、平移不改变图形的形状和大小 B、对顶角相等 C、两个直角一定互补 D、同位角相等7. 我市某中学举办了一次以“阳光少年,我们是好伙伴”为主题的演讲比赛,有9名同学参加了决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差8. 下列各数能整除 的是( )A、62 B、63 C、64 D、669. 如图, ,则 和 的关系是( )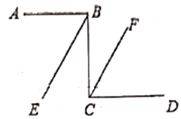 A、不是同位角但相等 B、是同位角且相等 C、是同位角但不相等 D、不是同位角也不相等10. 一副直角三角尺叠放如图1所示,现将 的三角尺 固定不动,将含 的三角尺 绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 ( )符合条件的其它所有可能度数为( )
A、不是同位角但相等 B、是同位角且相等 C、是同位角但不相等 D、不是同位角也不相等10. 一副直角三角尺叠放如图1所示,现将 的三角尺 固定不动,将含 的三角尺 绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 ( )符合条件的其它所有可能度数为( ) A、 和 B、 、 、 、 C、 和 D、以上都有可能
A、 和 B、 、 、 、 C、 和 D、以上都有可能二、填空题
-
11. 计算: .12. 计算 .13. 方程 , , , , 中是二元一次方程的是个.14. 已知多项式 是完全平方式,且 ,则m的值为 .15. 如图,若 ,则 、 、 之间的关系为.
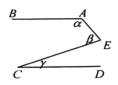 16. 已知直线 ,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是 .17. 把一张对边互相平行的纸条(AC′//BD′)折成如图所示,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,则∠AEG= .
16. 已知直线 ,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是 .17. 把一张对边互相平行的纸条(AC′//BD′)折成如图所示,EF是折痕,若折痕EF与一边的夹角∠EFB=32°,则∠AEG= .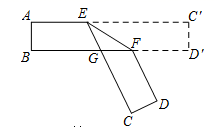 18. 与 的两边互相垂直,且 ,则 的度数为.
18. 与 的两边互相垂直,且 ,则 的度数为.三、解答题
-
19. 下列各式分解因式:(1)、(2)、20. 选择合适方法解下列方程组:(1)、(2)、21. 先化简,再求值: ,其中22. 如图,点 分别是边 上的点, , ,试说明 .

解:∵ ,( )
∴ ( )
∵ ( )
∴ ( )
∴ ( )
23.在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
 (1)、画出△DEF;(2)、连接AD、BE,则线段AD与BE的关系是;(3)、求△DEF的面积.
(1)、画出△DEF;(2)、连接AD、BE,则线段AD与BE的关系是;(3)、求△DEF的面积.
24. 某中学有15位学生利用暑假参加社会实践活动,到某公司销售部做某种商品的销售员,销售部为帮助学生制定合理的周销售定额,统计了这15位学生某周的销售量如下:周销售量(件)
450
130
60
50
40
35
人数
1
1
3
5
3
2
(1)、求这15位学生周销售量的平均数、中位数、众数;(2)、假设销售部把每位学生的周销售定额规定为80件,你认为是否合理?为什么?如果不合理,请你从表中选一个较合理的周销售量作为周销售定额,并说明理由.25. 在阿斯塔纳进行的2019国际象棋世界团体锦标赛当地时间14日落幕,中国女队以全胜战绩(八连胜)完美夺冠,中国队与俄罗斯队的对决尤为激烈,双方苦战15轮,最终中国队净胜俄罗斯队3分,比赛的积分规则是胜得1分,负得0分,和棋各得0.5分,问中国队与俄国斯队的积分各是多少?26. 如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.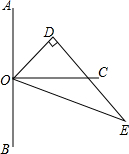 (1)、当OD在OA与OC之间,且∠COD=20°时,则∠AOE=;(2)、试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;(3)、在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
(1)、当OD在OA与OC之间,且∠COD=20°时,则∠AOE=;(2)、试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;(3)、在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.