山东省淄博市沂源县(五四制)2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-18 类型:期中考试
一、单选题
-
1. 下列各组数是勾股数的是( )A、12、15、18 B、6、8、12 C、4、5、6 D、7、24、252. 如图所示4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列结论正确的个数有( )
3. 下列结论正确的个数有( )①有两边和一角对应相等的两个三角形全等;
②三角形三边的垂直平分线相交于一点;
③有两边及夹角对应相等的两个三角形全等;
④三角形三个内角的角平分线有可能相交于三角形的外部.
A、0个 B、1个 C、2个 D、3个4. 下面是证明勾股定理的四个图形,其中是轴对称图形的是( )A、 B、
B、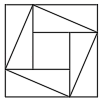 C、
C、 D、
D、 5. 图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
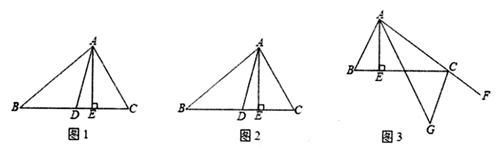
5. 图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )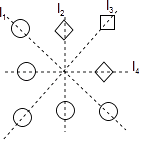 A、l1 B、l2 C、l3 D、l46. 下列说法中:①线段是轴对称图形,②成轴对称的两个图形对称点的连线互相平行,③等腰三角形的角平分线就是底边的垂直平分线,④已知两腰就能确定等腰三角形的形状和大小,正确的有( ).A、1个 B、2个 C、3个 D、4个7. 如图,在 中, , 是三角形的重心,那么图中全等的三角形的对数是( )
A、l1 B、l2 C、l3 D、l46. 下列说法中:①线段是轴对称图形,②成轴对称的两个图形对称点的连线互相平行,③等腰三角形的角平分线就是底边的垂直平分线,④已知两腰就能确定等腰三角形的形状和大小,正确的有( ).A、1个 B、2个 C、3个 D、4个7. 如图,在 中, , 是三角形的重心,那么图中全等的三角形的对数是( )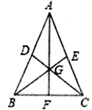 A、5 B、6 C、7 D、88. 下列命题中,正确的是( )A、形状相同的两个三角形是全等形 B、面积相等的两个三角形全等 C、周长相等的两个三角形全等 D、周长相等的两个等边三角形全等9. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b.若 ,大正方形的面积为25,则小正方形的边长为( )
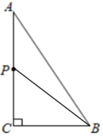
A、5 B、6 C、7 D、88. 下列命题中,正确的是( )A、形状相同的两个三角形是全等形 B、面积相等的两个三角形全等 C、周长相等的两个三角形全等 D、周长相等的两个等边三角形全等9. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a , 较短直角边长为b.若 ,大正方形的面积为25,则小正方形的边长为( )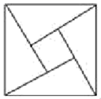 A、9 B、6 C、4 D、310. 如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
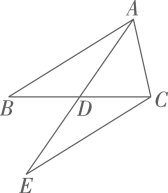
A、9 B、6 C、4 D、310. 如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( ) A、15° B、20° C、25° D、30°11. 如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )
A、15° B、20° C、25° D、30°11. 如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )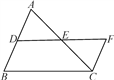 A、8 B、7 C、6 D、512. 如图, 的内角 平分线 与外角 的平分线交于点 ,过 作 分别交 于 两点.下列结论:① ;② ;③ ;④ ,其中正确的结论有( )
A、8 B、7 C、6 D、512. 如图, 的内角 平分线 与外角 的平分线交于点 ,过 作 分别交 于 两点.下列结论:① ;② ;③ ;④ ,其中正确的结论有( )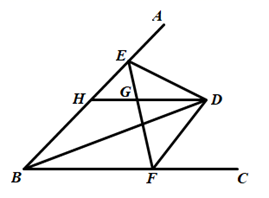 A、只有①②③ B、只有①②④ C、只有③④ D、①②③④
A、只有①②③ B、只有①②④ C、只有③④ D、①②③④二、填空题
-
13. 正三角形是轴对称图形,它有条对称轴14. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是.15. 如图,把长短确定的两根木棍 的一端固定在 处,和第三根木棍 摆出 ,木棍 固定,木棍 绕 转动,得到 ,这个实验说明 .
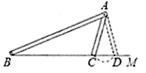 16. 《九章算术》是我国古代最重要的数学著作之一,在勾股章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折着高几何?”翻译成数学问题是:如图所示,在ΔABC中,∠ACB=90º, AC+AB=10, BC=3,求AC的长,若设AC=x, 则可列方程为.
16. 《九章算术》是我国古代最重要的数学著作之一,在勾股章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折着高几何?”翻译成数学问题是:如图所示,在ΔABC中,∠ACB=90º, AC+AB=10, BC=3,求AC的长,若设AC=x, 则可列方程为. 17. 如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计)
17. 如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计)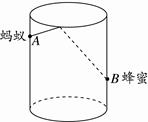
三、解答题
-
18. 如图, 的角平分线 相交于点 .
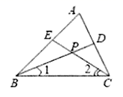 (1)、若 ,则 ;(2)、试探究 与 之间的数量关系并说明理由.19. 如图, , 为 的 边上的中线, 与 全等吗?为什么?
(1)、若 ,则 ;(2)、试探究 与 之间的数量关系并说明理由.19. 如图, , 为 的 边上的中线, 与 全等吗?为什么?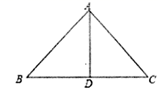 20. 在 中, 的垂直平分线 交 于点 , 的垂直平分线 交 于点 , 与 相交于点 , 的周长为6.
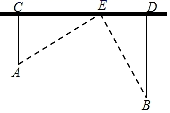
20. 在 中, 的垂直平分线 交 于点 , 的垂直平分线 交 于点 , 与 相交于点 , 的周长为6. (1)、 与 的数量关系为 .(2)、求 的长.(3)、分别连接 , , ,若 的周长为16,求 的长.21. 如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km , B村庄到公路的距离BD=14km , 测得C、D两点的距离为20km , 现要在CD之间建一个服务区E , 使得A、B两村庄到E服务区的距离相等,求CE的长.
(1)、 与 的数量关系为 .(2)、求 的长.(3)、分别连接 , , ,若 的周长为16,求 的长.21. 如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km , B村庄到公路的距离BD=14km , 测得C、D两点的距离为20km , 现要在CD之间建一个服务区E , 使得A、B两村庄到E服务区的距离相等,求CE的长.