山东省烟台市龙口市（五四制）2020-2021学年七年级上学期数学期中试卷
试卷更新日期：2020-12-18 类型：期中考试
一、单选题
-
1. 小强将一张正方形纸片按如图所示对折两次，并在如图位置上剪去一个小正方形，然后展开得到（ ）
A、
B、
C、
D、
2. 下列说法中正确的是（ ）A、轴对称图形是由两个图形组成的 B、等边三角形有三条对称轴 C、两个全等三角形组成一个轴对称图形 D、直角三角形一定是轴对称图形3. 如图所示的图形中， 于 ，线段AE是几个三角形的高（ ）．
A、3 B、4 C、5 D、64. 如图，AC＝BD，AO＝BO，CO＝DO，∠D＝30°，∠A＝95°，则∠AOB等于（ ）
A、120° B、125° C、130° D、135°5. 如图小明从平面镜里看到镜子对面电子钟显示的时间如图所示，这时的实际时刻应该是（ ）
A、21∶10 B、10∶21 C、10∶51 D、12∶016. 已知直角三角形的两条直角边长为6，8，那么斜边上的高为（ ）A、4.8 B、5 C、2 D、107. 如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，BC＝5，EF垂直平分BC，点P为直线EF上的任一点，则AP＋BP的最小值是（ ）
A、5 B、4 C、3 D、78. 有一张直角三角形纸片，两直角边长AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE（如图），则CD则等于（ ）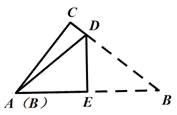
A、 B、 C、 D、9. 如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中能使△ABC≌△DEF的条件有（ ）
A、1组 B、2组 C、3组 D、4组10. 一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处．若M，N两点相距100海里，则∠NOF的度数为（ ）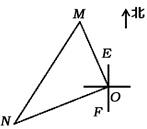
A、50° B、60° C、70° D、90°11. 将一根 的筷子，置于底面直径为 ，高 的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度 ，则 的取值范围是（ ）
A、 B、 C、 D、12. 如图，方格纸中有四个相同的正方形，则∠1+∠2+∠3为（ ）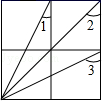
A、90° B、120° C、135° D、150°二、填空题
-
13. a，b，c为ΔABC的三边，化简|a-b-c|-|a+b-c|+2a结果是.14. 如图，△EFG≌△NMH，△EFG的周长为15cm，HN=6cm，EF=4cm，FH=1cm，则HG= ．
15. 已知△ABC中，AB=20，AC=15，BC边上的高为12，则△ABC的周长为 ．16. 如图，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，且S△ABC＝1cm2 ， 则S△BEF＝cm2 ．
17. 用直尺和圆规作一个角等于已知角的示意图，如图所示，则说明∠A′O′B′＝∠AOB的依据是全等三角形的相等．其全等的依据是 ．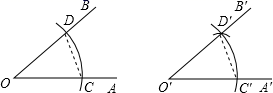
18. 如图，阴影部分是两个正方形，其它部分是两个直角三角形和一个正方形．若右边的直角三角形 中， ， ，则阴影部分的面积是 ．
三、解答题
-
19. 如图，在4×4的正方形网格中，每个小正方形的边长都是1，△ABC三个顶点分别在正方形网格的格点上，试判断△ABC是否是直角三角形．
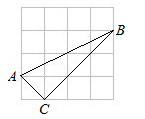20. 如图，在△ABC中，AB=AC，取点D与点E，使得AD=AE，∠BAE=∠CAD，连结BD与CE交于点O．求证：
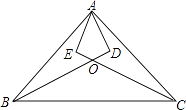(1)、△ABD≌△ACE；(2)、OB=OC．21. 如图，在Rt△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，DE⊥AB于点E.
(1)、求证：△ACD≌△AED(2)、若AC=5，△DEB的周长为8，求△ABC的周长22. 甲、乙两船同时从港口 出发，甲船以30海里/时的速度沿北偏东 方向航行，乙船沿南偏东 向航行，2小时后，甲船到达 岛，乙船到达 岛，若 ， 两岛相距100海里，问乙船的速度是每小时多少海里？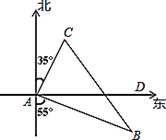
23.(1)、如图，在“4×4”正方形网格中，已有2个小正方形被涂黑．请你分别在下面2张图中再将若干个空白的小正方形涂黑，使得涂黑的图形成为轴对称图形．（图（1）要求只有1条对称轴，图（2）要求只有2条对称轴）．
（只有1条对称轴） （只有2条对称轴）
图⑴ 图⑵
(2)、如图，A、B为直线MN外两点，且到MN的距离不相等．分别在MN上求一点P ， 并满足如下条件：①在图⑶中求一点P使得PA+PB最小；②在图⑷中求一点P使得｜PA－PB｜最大．（不写作法，保留作图痕迹）
24. 有一辆装满货物的卡车，高2.5米，宽1.6米，要开进如图所示的上边是半圆，下边是长方形的桥洞，已知半圆的直径为2米，长方形的另一条边长是2.3米.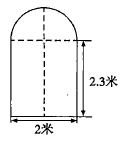
(1)、这辆卡车能否通过此桥洞？试说明你的理由.(2)、为了适应车流量的增加，想把桥洞改为双行道，并且要使宽1.2米，高为2.8米的卡车能安全通过，那么此桥洞的宽至少应增加到多少米？25. 如图，已知在等腰直角三角形△DBC中，∠BDC=90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA=DF，
(1)、试说明：△FBD≌△ACD；(2)、延长BF交AC于E，且BE⊥AC，试说明： ；(3)、在（2）的条件下，若H是BC边的中点，连接DH与BE相交于点G．试探索CE，GE，BG之间的数量关系，并说明理由．