山东省临沂市兰山区2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-18 类型:期中考试
一、单选题
-
1. 实数﹣ 的相反数是( )A、 B、﹣ C、2 D、﹣22. 若足球质量与标准质量相比,超出部分记作正数,不足部分记作负数,则在下面4个足球中,质量最接近标准的是A、
 B、
B、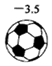 C、
C、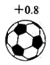 D、
D、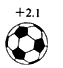 3. 这段时间,一个叫“学习强国”的理论学习平台火了,很多人主动下载、积极打卡,兴起了一股全民学习的热潮.据不完全统计,截止4月2号,华为官方应用市场“学习强国APP”下载量已达8830万次,请将8830万用科学记数法表示为( )A、0.883×109 B、8.83×108 C、8.83×107 D、88.3×1064. 下列说法中,正确的是( )A、 是单项式 B、﹣5不是单项式 C、﹣πx2的系数为﹣1 D、﹣πx2的次数为25. 下列各式中,不是同类项的是( )A、﹣2019和2020 B、a和π C、﹣4x3y2和5x3y2 D、a2b和﹣3ba26. 若数轴上点A表示的数是-3,则与点A相距4个单位长度的点表示的数是( )A、±4 B、±1 C、-7或1 D、-1或77. 设x,y,c是实数,下列说法正确的是( )A、若x=y,则xc=yc B、若x=y,则x+c=y﹣c C、若x=y,则 D、若 ,则2x=3y8. 下列去括号正确的是( )A、a+(-3b+2c-d)=a-3b+2c-d B、-(-x2+y2)=-x2-y2 C、a2-(2a-b+c)=a2-2a-b+c D、a-2(b-c)=a+2b-c9. 若 满足 则 的值是( )A、1 B、-1 C、2019 D、-201910. 观察图中正方形四个顶点所标的数字规律,可知数2020应标在( )
3. 这段时间,一个叫“学习强国”的理论学习平台火了,很多人主动下载、积极打卡,兴起了一股全民学习的热潮.据不完全统计,截止4月2号,华为官方应用市场“学习强国APP”下载量已达8830万次,请将8830万用科学记数法表示为( )A、0.883×109 B、8.83×108 C、8.83×107 D、88.3×1064. 下列说法中,正确的是( )A、 是单项式 B、﹣5不是单项式 C、﹣πx2的系数为﹣1 D、﹣πx2的次数为25. 下列各式中,不是同类项的是( )A、﹣2019和2020 B、a和π C、﹣4x3y2和5x3y2 D、a2b和﹣3ba26. 若数轴上点A表示的数是-3,则与点A相距4个单位长度的点表示的数是( )A、±4 B、±1 C、-7或1 D、-1或77. 设x,y,c是实数,下列说法正确的是( )A、若x=y,则xc=yc B、若x=y,则x+c=y﹣c C、若x=y,则 D、若 ,则2x=3y8. 下列去括号正确的是( )A、a+(-3b+2c-d)=a-3b+2c-d B、-(-x2+y2)=-x2-y2 C、a2-(2a-b+c)=a2-2a-b+c D、a-2(b-c)=a+2b-c9. 若 满足 则 的值是( )A、1 B、-1 C、2019 D、-201910. 观察图中正方形四个顶点所标的数字规律,可知数2020应标在( ) A、第505个正方形的左下角 B、第505个正方形的右下角 C、第506个正方形的右下角 D、第506个正方形的左下角
A、第505个正方形的左下角 B、第505个正方形的右下角 C、第506个正方形的右下角 D、第506个正方形的左下角二、填空题
-
11. 已知多项式 ,它是次三项式,最高次项的系数 , 常数项为 .12. 如果 ,那么 等于.13. 绝对值大于4而小于7的所有整数之和是.14. 已知关于x的方程3x-2k=2的解是x=2,则k的值是 .15. 一个两位数,个位数字为a , 十位数字为b , 把这个两位数的个位数字与十位数字交换,得到新的两位数,则新数比原数大 .16. 若 , ,则 .
三、解答题
-
17. 在数轴上表示下列各数,并将它们用“>”连接:
, , , ,
18. 计算:(1)、 ;(2)、19. 先化简,再求值: ,其中 .20. 临沂兰山区李官镇的黄桃闻名全国.现有20筐黄桃,以每筐25千克为标准,超过或不足的千克数分别用正数或负数来表示,记录如下:与标准质量的差值(单位:千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)、与标准重量比较,20筐黄桃总计超过或不足多少千克?(2)、若黄桃每千克售价4元,则这20筐可卖多少元?21. 如图所示,池塘边有块长为20m , 宽为10m的长方形土地,现在将其余三面留出宽都是x m的小路,中间余下的长方形部分做菜地.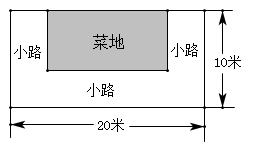 (1)、用含x的式子表示菜地的周长;(2)、求当x=1m时,菜地的周长.22. 某工厂第一车间有 人,第二车间比第一车间人数的 少30人,如果从第二车间调出10人到第一车间,那么(1)、两个车间共有人.(2)、调动后,第一车间的人数为人,第二车间的人数为人.(3)、求调动后,第一车间的人数比第二车间的人数多几人?23. 某电器上销售一种微波炉和电磁炉,微波炉每台定价 元,电磁炉每台定价 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
(1)、用含x的式子表示菜地的周长;(2)、求当x=1m时,菜地的周长.22. 某工厂第一车间有 人,第二车间比第一车间人数的 少30人,如果从第二车间调出10人到第一车间,那么(1)、两个车间共有人.(2)、调动后,第一车间的人数为人,第二车间的人数为人.(3)、求调动后,第一车间的人数比第二车间的人数多几人?23. 某电器上销售一种微波炉和电磁炉,微波炉每台定价 元,电磁炉每台定价 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的 付款;
现某客户要到该卖场购买微波炉 台,电磁炉 台
(1)、若该客户按方案一、方案二购买,分别需付款多少元?(用含 的式子表示)(2)、若 ,通过计算说明此时那种方案购买较为核算?(3)、当 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?