山东省济南外国语2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-18 类型:期中考试
一、单选题
-
1. -2020的绝对值是( )A、-2020 B、2020 C、 D、2. 在﹣4, ,0,3.14159,﹣5.2,2中正有理数的个数有( )A、1个 B、2个 C、3个 D、4个3. 用一个平面去截下列几何体,截得的平面图形不可能是三角形的是( )A、
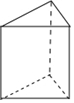 B、
B、 C、
C、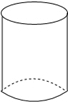 D、
D、 4. 2020年国庆档电影《我和我的家乡》通过讲述中国东西南北中五大地域的家乡故事,抒发人们的家国情怀,展示脱贫攻坚成果.该电影上映第一天票房为10500万元,则数字10500用科学记数法可表示为( )A、 B、 C、 D、5. 一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的元件是( )A、
4. 2020年国庆档电影《我和我的家乡》通过讲述中国东西南北中五大地域的家乡故事,抒发人们的家国情怀,展示脱贫攻坚成果.该电影上映第一天票房为10500万元,则数字10500用科学记数法可表示为( )A、 B、 C、 D、5. 一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的元件是( )A、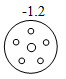 B、
B、 C、
C、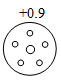 D、
D、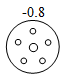 6. 下列算式中,运算结果为负数的是( )A、 B、 C、 D、7. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )
6. 下列算式中,运算结果为负数的是( )A、 B、 C、 D、7. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )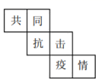 A、 共 B、同 C、疫 D、情8. 下列各式,运算正确的是( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、单项式 的系数 B、单项式 的次数为-5 C、多项式 是二次三项式 D、多项式 的常数项是110. 已知有理数a,b,c在数轴上的位置如图所示,下列结论正确的是( )
A、 共 B、同 C、疫 D、情8. 下列各式,运算正确的是( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、单项式 的系数 B、单项式 的次数为-5 C、多项式 是二次三项式 D、多项式 的常数项是110. 已知有理数a,b,c在数轴上的位置如图所示,下列结论正确的是( ) A、 B、 C、 D、11. 某校在疫情复学后建立了一个身份识别系统,利用如图 的二维码可以进行身份识别,图 是某个学生的识别图案,黑色小正方形表示 白色小正方形表示0,将第一行小正方形表示的数字从左到右依次记为 那么可以转换为该生所在班级序号,其序号为 如图 第一行小正方形表示的数字从左到右依次为 ,序号为 表示该生为 班学生.表示 班学生的识别图案是( )
A、 B、 C、 D、11. 某校在疫情复学后建立了一个身份识别系统,利用如图 的二维码可以进行身份识别,图 是某个学生的识别图案,黑色小正方形表示 白色小正方形表示0,将第一行小正方形表示的数字从左到右依次记为 那么可以转换为该生所在班级序号,其序号为 如图 第一行小正方形表示的数字从左到右依次为 ,序号为 表示该生为 班学生.表示 班学生的识别图案是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、
12. 已知有理数 ,我们把 称为 的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 , 是 的差倒数, 是 的差倒数, 是 的差倒数…依此类推,那么 的值是( )A、-3 B、 C、 D、二、填空题
-
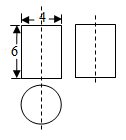
13. 我市某天的最高气温是4℃,最低气温是 ,则这天的日温差是℃.14. 单项式2xmy3与﹣3xy3n是同类项,则m+n=.15. 比较两数的大小: (填“>”或“<”)16. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).
 17. 按照如图所示的计算程序,若 ,则输出的结果是.
17. 按照如图所示的计算程序,若 ,则输出的结果是.
 18. 如图是用棋子摆成的“ ”字图案.从图案中可以看出,第1个“ ”字图案需要4枚棋子,第2个“ ”字图案需要7枚棋子,第3个“ ”字图案需要10枚棋子.照此规律,摆成第 个“ ”字图案需要2020枚棋子,则 的值为 .
18. 如图是用棋子摆成的“ ”字图案.从图案中可以看出,第1个“ ”字图案需要4枚棋子,第2个“ ”字图案需要7枚棋子,第3个“ ”字图案需要10枚棋子.照此规律,摆成第 个“ ”字图案需要2020枚棋子,则 的值为 . 19. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .20. 定义运算x★y= ,则共 100个★的计算结果是 .21. 对于一个数 ,我们用 表示小于 的最大整数 ,例如: , ,如果 ,则 的取值范围为 .22. 将7张相同的小长方形纸片(如图1所示)按图2所求的方式不重叠的放在长方形 内,未被覆盖的部分恰好被分割为两个长方形,面积分别为 ,已知小长方形纸片的长为 ,宽为 ,且 .若 长度不变, 变长,将这7张小长方形纸片还按照同样的方式放在新的长方形 内,而 的值总保持不变,则 满足的关系是 .
19. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .20. 定义运算x★y= ,则共 100个★的计算结果是 .21. 对于一个数 ,我们用 表示小于 的最大整数 ,例如: , ,如果 ,则 的取值范围为 .22. 将7张相同的小长方形纸片(如图1所示)按图2所求的方式不重叠的放在长方形 内,未被覆盖的部分恰好被分割为两个长方形,面积分别为 ,已知小长方形纸片的长为 ,宽为 ,且 .若 长度不变, 变长,将这7张小长方形纸片还按照同样的方式放在新的长方形 内,而 的值总保持不变,则 满足的关系是 .
三、解答题
-
23. 计算:(1)、(2)、24. 先化简,再求值: ,其中 .25. 如图是一些棱长为 的小立方块组成的几何体.请你画出从正面看,从左面看,从上面看到的这个几何体的形状图.
 26.(1)、(2)、27. 有三个有理数 ,已知 ( 为正整数),且 与 互为相反数,b与c互为倒数.(1)、当 n=2020 时,a= , b= , c=;(2)、当 n=2021 时,a= , b= , c= ;(3)、若 是最大的负整数,则 = .28. 2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个)
26.(1)、(2)、27. 有三个有理数 ,已知 ( 为正整数),且 与 互为相反数,b与c互为倒数.(1)、当 n=2020 时,a= , b= , c=;(2)、当 n=2021 时,a= , b= , c= ;(3)、若 是最大的负整数,则 = .28. 2020年的“新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩厂为满足市场需求计划每天生产5000个,由于各种原因实际每天生产量相比有出入,下表是二月份某一周的生产情况(超产为正,减产为负,单位:个)星期
一
二
三
四
五
六
日
增减
+100
-200
+400
-100
-100
+350
+150
(1)、根据记录可知前三天共生产多少个口罩?(2)、产量最多的一天比产量最少的一天多生产多少个?(3)、该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总金额是多少元?29. 如图,一个大长方形中剪下两个大小相同的小长方形(有关线段的长如图所示),留下一个“ ”型的图形(阴影部分). (1)、用含 的代数式表示阴影部分的周长;(2)、用含 的代数式表示阴影部分的面积;(3)、当 时,计算阴影部分的面积.30. (概念学习)
(1)、用含 的代数式表示阴影部分的周长;(2)、用含 的代数式表示阴影部分的面积;(3)、当 时,计算阴影部分的面积.30. (概念学习)规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如 等.类比有理数的乘方,我们把 记作 ,读作“2的下3次方”,一般地,把 个 相除记作 ,读作“ 的下 次方”.
(1)、(初步探究)直接写出计算结果: .
(2)、关于除方,下列说法正确的选项有(只需填入正确的序号);①任何非零数的下2次方都等于1;
②对于任何正整数 , ;
③ ;
④负数的下奇数次方结果是负数,负数的下偶数次方结果是正数.
(3)、(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
例如: (幂的形式)
试一试:将下列除方运算直接写成幂的形式.56 ; = ;
(4)、算一算:31. 如图:在数轴上 点表示数 , 点表示数 , 点表示数 ,且 , 满足 , , (1)、 , ;(2)、若将数轴折叠,使得 点与 点重合,则点 与数表示的点重合.(3)、在(1)(2)的条件下,若点 为数轴上一动点,其对应的数为 ,当代数式 取得最小值时,此时 , 最小值为.(4)、在(1)(2)的条件下,若在点 处放一挡板,一小球甲从点 处以 个单位 秒的速度向左运动;同时另一小球乙从点 处以 个单位 秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为 (秒),请表示出甲、乙两小球之间的距离 (用 的代数式表示)
(1)、 , ;(2)、若将数轴折叠,使得 点与 点重合,则点 与数表示的点重合.(3)、在(1)(2)的条件下,若点 为数轴上一动点,其对应的数为 ,当代数式 取得最小值时,此时 , 最小值为.(4)、在(1)(2)的条件下,若在点 处放一挡板,一小球甲从点 处以 个单位 秒的速度向左运动;同时另一小球乙从点 处以 个单位 秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为 (秒),请表示出甲、乙两小球之间的距离 (用 的代数式表示)