内蒙古自治区北京四中呼和浩特分校2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2020-12-18 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $- (- 8), {(- 1)}^{2014}, - 3^{2}, - 1, - | - 3 |$ 中，负数共有（）

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
2. 下列说法：①-a一定是负数；②倒数等于它本身的数是 $\pm 1$ ；③绝对值等于它本身的数是正数；④平方等于它本身的数是 $1$ ．其中说法正确的个数是（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 已知x=2是关于x的方程 $x - 7 m = 2 x + 5$ 的解，则m的值是（）

A、1 B、 $- 1$ C、7 D、 $- 7$

查看试题解析
4. 已知ax=ay ，下列等式不一定成立的是（）

A、x=y B、b+ax=b+ay C、x-ax=x-ay D、 $\frac{a x}{a^{2} + 1} = \frac{a y}{a^{2} + 1}$

查看试题解析
5. 下列说法错误的是（）

A、数字0是单项式 B、 $\frac{π x y^{2}}{3}$ 的系数是 $\frac{1}{3}$ ，次数是3 C、 $\frac{1}{4} a b$ 是二次单项式 D、 $\frac{2 m n}{5}$ 的系数是 $\frac{2}{5}$ ，次数是2

查看试题解析
6. 下列各组数互为相反数的是（）

A、 $3^{2}$ 与 $- 2^{3}$ B、 $3^{2}$ 与 ${(- 3)}^{2}$ C、 $3^{2}$ 与 $- 3^{2}$ D、 $- 2^{3}$ 与 ${(- 2)}^{3}$

查看试题解析
7. 下列说法正确的是（）

A、近似数 $5$ 千和 $500$ 的精确度是相同的 B、 $317500$ 精确到千位可以表示为 $31.8$ 万，也可以表示为： $3.18 \times 10^{5}$ C、 $2.46$ 万精确到百分位 D、近似数 $8.4$ 和 $0.7$ 的精确度不一样

查看试题解析
8. 一根1米长的绳子，第一次剪去它的三分之一，如此剪下去，第五次后剩下的绳子的长度为（）

A、 ${(\frac{2}{3})}^{4}$ 米 B、 ${(\frac{2}{3})}^{5}$ 米 C、 ${(\frac{2}{3})}^{6}$ 米 D、 ${(\frac{2}{3})}^{10}$ 米

查看试题解析
9. 已知代数式 $3 x^{2} - 4 x$ 的值为 $9$ ，则 $6 - 9 x^{2} + 12 x$ 的值为（）

A、 $3$ B、 $24$ C、 $- 21$ D、 $18$

查看试题解析
10. 下列说法正确的有（）
① $| a - b | = a - b$ ,则 $a \geq b$ ；②数轴上到某点距离相等的两个点对应的数相等

③ $a b c < 0$ ,则 $\frac{a b}{| a b |} + \frac{b c}{| b c |} + \frac{a c}{| a c |} + \frac{| a b c |}{a b c} = \pm 2$ ；④ $| a + b | = | a - b |,$ 则 $b = 0$

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若 $- x^{m} y^{4}$ 与 $\frac{1}{12} x^{3} y^{n}$ 是同类项，则 ${(m - n)}^{9}$ = ．

查看试题解析
12. 已知关于 $x$ 的方程 $(m^{2} - 4) x^{2} - (m + 2) x - 3 = 0$ 是一元一次方程，则 $m =$ ，该方程的解为 $x =$ ．

查看试题解析
13. 若关于 $a, b$ 的多项式 $- 2 a b + \frac{1}{3} k a^{2} b + 5 b^{2}$ 与 $b^{2} + 3 a^{2} b - 5 a b + 1$ 的差不含三次项，则数 $k$ 的值为．

查看试题解析
14. 一只蚂蚁从数轴上一点 A出发，爬了7 个单位长度到了+1，则点 A 所表示的数是

查看试题解析
15. 在数轴上的对应点的位置如图所示，化简 $| b - c | + | a + b | - | a |$ 的结果是．

查看试题解析
16. 为了拓展销路，商店对某种照相机的售价作了调整，按原价的8折(标价的80%)出售，此时的利润率为14%，若此种照相机的进价为1200元，问该照相机的原售价是．

查看试题解析
17. 数学兴趣活动小组的同学们用棋子摆了如图的三个“工”字形图案．依照这种规律摆放，摆第 $4$ 个“工”字形图案需个棋子；摆第 $n$ 个“工”字形图案需个棋子．

查看试题解析
18. 定义一种运算： $a * b = \frac{1}{a + b} + \frac{x}{(a + 1) (b + 1)}$ ，若设 $2 * 1 = \frac{5}{3}$ ，则 $3 * 4 =$ .

查看试题解析

三、解答题

19.

(1)、 $(+ 17 \frac{3}{4}) - (+ 6.25) - (- \frac{1}{2}) + (- 0.75) - (+ 22 \frac{1}{4})$

(2)、 $5 - 3 \div 2 \times \frac{1}{2} - | - 2 | \div (- \frac{1}{2})$

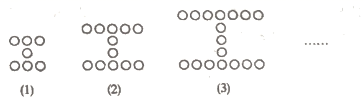(3)、 $- 3^{2} + 3 \times {(- 1)}^{2018} - (\frac{3}{8} + \frac{1}{6} - \frac{3}{4}) \times {(- 2)}^{2}$

查看试题解析
20. 用等式性质解方程
$\frac{4}{3} x - \frac{1}{2} = \frac{1}{2} x + \frac{1}{2}$

查看试题解析
21. 已知多项式 $a x^{5} + b x^{3} + 3 x + c$ ，当 $x = 0$ 时，该式的值为 $- 1$ ．

(1)、求c的值；

(2)、若当x=1时，该式的值为 $- 1$ ，试求 $a + b + c$ 的值；

(3)、若当 $x = 3$ 时，该式的值为 $- 10$ ，试求当 $x = - 3$ 时该式的值．

查看试题解析
22. 在做解方程练习时，学习卷中有一个方程“2y– $\frac{1}{2}$ = $\frac{1}{2}$ y+■”中的■没印清晰，小聪问老师，老师只是说：“■是一个有理数，该方程的解与当x=2时代数式5（x–1）–2（x–2）–4的值相同．”小聪很快补上了这个常数．同学们，你们能补上这个常数吗？

查看试题解析
23. 已知数a在数轴上表示的点在原点左侧，距离原点3个单位长，b在数轴上表示的点在原点右侧，距离原点2个单位长，c和d互为倒数，m与n互为相反数，y为最大的负整数，求 $(y + b^{2}) + m (a - c d) - n b^{2}$ 的值.

查看试题解析
24. 已知 $A = 3 a^{2} b - 3 a b^{2} + 4 a b c$ ，小明错将“ $2 A - B$ ”看成“ $2 A + B$ ”，算得结果 $C = 4 a^{2} b - 3 a b^{2} + 4 a b c$ ．

(1)、计算 $B$ 的表达式；

(2)、求正确的结果的表达式．

查看试题解析
25. 世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+10，﹣2，+5，﹣6，+12，﹣9，+4，﹣14.（假定开始计时时，守门员正好在球门线上）

(1)、守门员最后是否回到球门线上？

(2)、守门员离开球门线的最远距离达多少米？

(3)、如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门.请问在这一时间段内，对方球员有几次挑射破门的机会？

查看试题解析
26. 已知， $A ， B$ 在数轴上对应的数分别用 $a ， b$ 表示，且 ${(\frac{1}{2} a b + 100)}^{2} + | a - 20 | = 0 ， P$ 是数轴上的一个动点．

(1)、在数轴上标出 $A ， B$ 的位置，并求出 $A ， B$ 之间的距离．

(2)、已知数轴上在点 $O$ 与点 $B$ 之间有点 $C$ ，且 $B$ 与 $C$ 的距离是 $6$ ，当数轴上有点 $P$ 满足 $P$ 与 $B$ 的距离等于 $P$ 与 $C$ 的距离的 $2$ 倍时，求 $P$ 点对应的数．

查看试题解析