江西省吉安市七校联盟2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-18 类型:期中考试
一、单选题
-
1. 在 中,最小的数是( )A、 B、 C、 D、2. 如图是正方体的表面展开图,则与“前”字相对的字是( )
 A、认 B、真 C、复 D、习3. 下列说法正确的是A、单项式 的系数0,次数是2 B、单项式 的系数 ,次数是5 C、 , ,5是多项式 的项 D、 是二次二项式4. 如图所示的几何体的从左面看到的图形为( )
A、认 B、真 C、复 D、习3. 下列说法正确的是A、单项式 的系数0,次数是2 B、单项式 的系数 ,次数是5 C、 , ,5是多项式 的项 D、 是二次二项式4. 如图所示的几何体的从左面看到的图形为( )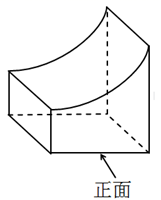 A、
A、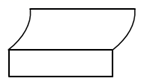 B、
B、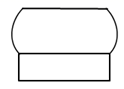 C、
C、 D、
D、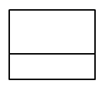 5. 化简 ( )A、 B、 C、 或 D、6. 一列数 ,其中 …, .则 … 的结果为( )A、 B、 C、 D、
5. 化简 ( )A、 B、 C、 或 D、6. 一列数 ,其中 …, .则 … 的结果为( )A、 B、 C、 D、二、填空题
-
7. 如果一个棱柱是由 个面围成的,那么这个棱柱是棱柱.8. 2020年“五一”假日期间,我省银联网络交易总金额接近 亿元.其中 亿用科学记数法表示为 .9. 笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说.10. 已知|a+3|+(b-1)2=0,则3a+b= .11. 若两个单项式 与 的和是 ,代数式 的值为 .12. 若a,b,c都不为0,则 的值可能是 .
三、解答题
-
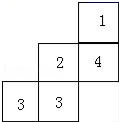
13. 计算(1)、(2)、14. 先化简,再求值: ,其中 .15. 某检修小组乘一辆汽车沿东西方向的公路检修线路,约定向东走为正,向西走为负.某天从 地出发到收工时,行走记录如下(单位:km): .(1)、收工时,检修小组在 地的哪一边,距 地多远?(2)、若汽车每千米耗油 ,已知汽车出发时油箱有 汽油,问收工前是否需要在中途加油?若加,应加多少升?若不加,还剩多少升汽油?16. 一个几何体由几个大小相同的小立方块搭成,从上面看这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面,左侧面看到的几何体的形状图.
 17. 已知n棱柱中的棱长都是 且该棱柱共有12个顶点.(1)、该棱柱的底面是边形;(2)、求该棱柱所有棱长的和及棱柱侧面展开图的面积.18. 初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.(1)、若有m名学生,用代数式表示两种优惠方案各需多少元?(2)、当m=70时,采用哪种方案优惠?19. 定义一种新运算:观察下列各式: .(1)、请你想一想:(2)、若 ,那么 (填“ ”或“ ”)(3)、先化简,再求值: ,其中 .20. 观察图示,解答问题.
17. 已知n棱柱中的棱长都是 且该棱柱共有12个顶点.(1)、该棱柱的底面是边形;(2)、求该棱柱所有棱长的和及棱柱侧面展开图的面积.18. 初一年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元,现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都7.5折收费.(1)、若有m名学生,用代数式表示两种优惠方案各需多少元?(2)、当m=70时,采用哪种方案优惠?19. 定义一种新运算:观察下列各式: .(1)、请你想一想:(2)、若 ,那么 (填“ ”或“ ”)(3)、先化简,再求值: ,其中 .20. 观察图示,解答问题. (1)、由上而下第 行,白球有个,黑球有个;(2)、若第 ( 为正整数)行白球与黑球的总数记作 ,求 与 的关系式;(3)、求出第 行白球和黑球的总数.21. 阅读材料:我们知道, ,类似地,我们把 看成一个整体,则 .“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
(1)、由上而下第 行,白球有个,黑球有个;(2)、若第 ( 为正整数)行白球与黑球的总数记作 ,求 与 的关系式;(3)、求出第 行白球和黑球的总数.21. 阅读材料:我们知道, ,类似地,我们把 看成一个整体,则 .“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
(1)、把 看成一个整体,合并 的结果是 .(2)、已知 ,求 的值;(3)、拓广探索:已知 ,求 的值.
22. 请同学们仔细阅读下列步骤,完成问题:①任意写一个三位数,百位数字比个位数字大2;
②交换百位数字与个位数字,得到一个三位数;
③用上述的较大的三位数减去较小的三位数,所得的差为三位数;
④交换这个差的百位数字与个位数字又得到一个三位数;
⑤把③④中的两个三位数相加,得到最后结果.
问题:
(1)、③中的三位数是;④中的三位数是;⑤中的结果是 .(2)、在草稿纸上试一个不同的三位数,看看结果是否都一样?如果一样,请你用含a、b的代数式表示这个三位数,解释其中的原因.23. 数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:点 在数轴上分别对应的数为 .则 两点间的距离表示为根据以上知识解题:
已知数轴上 两点对应的数分别为 和 为数轴上一点,对应的数为 .
(1)、线段 的长度可表示为(用含 的式子表示).(2)、在数轴上是否存在点 使得 ?若存在,求出 的值;若不存在,请说明理由;(3)、当 为线段 的中点时,点 同时开始在数轴上分别以每秒 个单位长度,每秒 个单位长度,每秒 个单位长度沿数轴正方向运动,试问经过几秒, ?