初中数学人教版九年级上学期期末专题复习专题:09 弧长及扇形的面积
试卷更新日期:2020-12-18 类型:复习试卷
一、单选题
-
1. 如图,半径为10的扇形 中, , 为弧AB上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
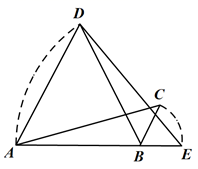
 A、 B、 C、 D、2. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、 B、 C、 D、2. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )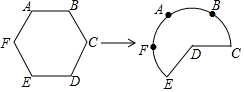 A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S23. 如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为( )
A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S23. 如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=12,且AC+BC=10,则AB的长为( ) A、 B、 C、 D、4. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( )
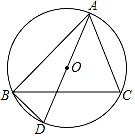
A、 B、 C、 D、4. 如图,半径为10的扇形 中, , 为 上一点, , ,垂足分别为 、 .若 为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、5. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( )
A、 B、 C、 D、5. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 在扇形OAB中,半径OA=2,S扇形OAB=π,则圆心角∠AOB=.
 7. 若一个扇形的弧长是 ,面积是 ,则扇形的圆心角是度.8. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,现在从第一个位置翻滚到第三个位置,则B点所经过的路径长度为.
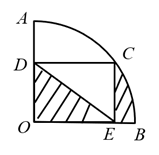
7. 若一个扇形的弧长是 ,面积是 ,则扇形的圆心角是度.8. 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,现在从第一个位置翻滚到第三个位置,则B点所经过的路径长度为.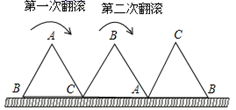 9. 如图,一张半径为2的圆型纸片在边长为a(a≥6)的正方形内任意移动,则在该正方形内,这张圆型纸片“不能接触到的部分”的面积是.
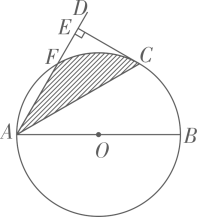
9. 如图,一张半径为2的圆型纸片在边长为a(a≥6)的正方形内任意移动,则在该正方形内,这张圆型纸片“不能接触到的部分”的面积是. 10. 如图,⊙O是 的外接圆, , ,则 的长为.
10. 如图,⊙O是 的外接圆, , ,则 的长为.
三、作图题
-
11. 在平面直角坐标系中, 的位置如图所示,其中 , , .
 (1)、画出 绕点 顺时针旋转 后得到的 ;(2)、求旋转过程中动点 所经过的路径长(结果保留 ).
(1)、画出 绕点 顺时针旋转 后得到的 ;(2)、求旋转过程中动点 所经过的路径长(结果保留 ).四、综合题