湖北省十堰市房县2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-12-17 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 方程x2＝x的解为（  ）
    A、x＝1 B、x＝1，x2＝－1 C、x1＝1，x2＝0 D、以上答案都不对

    查看试题解析

  • 2. 下列图案中，是中心对称图形的是（  ）
    A、 B、 C、 D、

    查看试题解析

  • 3.

    如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为（　　）

    A、45°  B、50° C、60° D、75°

    查看试题解析

  • 4. 用配方法将方程 x2- 4x-2= 0 变形为（x- 2）2=m 的过程中， m的值是（  ）
    A、7 B、6 C、5 D、4

    查看试题解析

  • 5. 将抛物线y＝x2向左平移1个单位长度，再向上平移2个单位长度所得的解析式为（  ）
    A、y=（x-1）2+2 B、y=（x+1）2-2 C、y=（x-1）2-2 D、y=（x+1）2+2

    查看试题解析

  • 6. 下列说法错误的是（　　）

    A、直径是圆中最长的弦 B、长度相等的两条弧是等弧 C、面积相等的两个圆是等圆 D、半径相等的两个半圆是等弧

    查看试题解析

  • 7. 二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（   ）

    A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限

    查看试题解析

  • 8. 填在下面各正方形中四个数之间都有相同的规律，根据这种规律m的值为（  ）

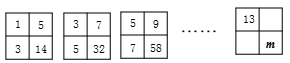    A、182 B、184 C、236 D、242

    查看试题解析

  • 9. 如图，已知AB是半圆⊙O的直径，∠DAC=27°，D是弧AC的中点，那么∠BAC的度数是（  ）

    A、46° B、36° C、29° D、32°

    查看试题解析

  • 10. 已知抛物线 y=ax2+bx+c （a＜0）的对称轴为 x＝－1，与 x 轴的一个交点为（3，0）.若关于 x 的一元二次方程 ax2+bx+c=p （p＞0）有整数根，则p的值有（  ）
    A、4个 B、3个 C、7个 D、5个

    查看试题解析

二、填空题

  • 11. 已知抛物线y=ax2+bx+8经过点（3，2），则代数式3a+b+8的值为.

    查看试题解析

  • 12. 在一个不透明的口袋中，装有4个红球和若干个白球，这些球除颜色外其余都相同，如果摸到红球的概率是 14 ，那么口袋中有白球个

    查看试题解析

  • 13. 如图，在半径为 5 的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=4，则OP的长为

    查看试题解析

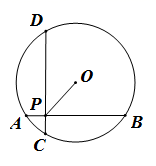  • 14. 对于两个不相等的实数a，b，我们规定符号Max{a，b}表示a，b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{x，-x}=x2-2的解为.

    查看试题解析

  • 15. 如图，将抛物线y=−12x2平移得到抛物线m.抛物线m经过点A（6，0）和原点O，它的顶点为P，它的对称轴与抛物线y=−12x2交于点Q，则图中阴影部分的面积为.

    查看试题解析

  • 16. 如图，正方形 ABCD 中，点 E 是 CD 边上一点，连接 AE，过点 B 作 BG⊥AE 于点 G， 连接 CG 并延长交 AD 于点 F，当 AF 的最大值是 2 时，正方形 ABCD 的边长为.

    查看试题解析

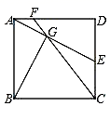
三、解答题

  • 17. 解方程：
    (1)、x2－6x＋7＝0
    (2)、（x－2）（x－5）＝－2.

    查看试题解析

  • 18. 已知二次函数y = 2x2 -4x -6.

    (1)、写出对称轴和顶点坐标.
    (2)、在平面直角坐标系中，画出这个二次函数的图象；
    (3)、当0<x<4时，求y的取值范围；

    查看试题解析

  • 19. 如图，某地新建的一座圆弧形的拱桥，正常水位时，水面宽40米，拱高10米，今年夏季汛期受上游涨水影响，水位持续上涨5米达到警戒水位，求此时水面的宽度.

    查看试题解析

  • 20. 某小学学生较多，为了便于学生尽快就餐，师生约定：早餐一人一份，一份两样，一样一个，食堂师傅在窗口随机发放（发放的食品价格一样），食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品．
    (1)、按约定，“小李同学在该天早餐得到两个油饼”是事件；（可能，必然，不可能）
    (2)、请用列表或树状图的方法，求出小张同学该天早餐刚好得到猪肉包和油饼的概率．

    查看试题解析

  • 21. 已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 ， x2 ．

    (1)、求m的取值范围；

    (2)、当x12+x22=6x1x2时，求m的值．

    查看试题解析

  • 22. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

    (1)、求证：BC是⊙O的切线；
    (2)、若⊙O的半径为 5 ，OP=1，求BC的长．

    查看试题解析

  • 23. 我校九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元.

    时间x（天）

    1≤x<50

    50≤x≤90

    售价（元/件）

    x+40

    90

    每天销量（件）

    200-2x
    (1)、求出y与x的函数关系式；
    (2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？
    (3)、该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.

    查看试题解析

  • 24. 如图1，E是正方形ABCD中CD边上的一点，以点A为中心，把 △ADE 顺时针旋转α后，得到 △ABG .

    (1)、求α的值；
    (2)、当点F在BC上，且∠EAF=45°，连接EF（如图2），求证：BF+DE=EF；
    (3)、在（2）的前提下，连接BD，分别交AE，AF于M，N两点（如图3），试判断线段BN，MN，DM三者的关系式，请给出证明.

    查看试题解析

  • 25. 如图，抛物线y = 13 x2−mx+n与x轴交于A，B两点，与y轴交于点C（0，−1）.且对称轴x=1.

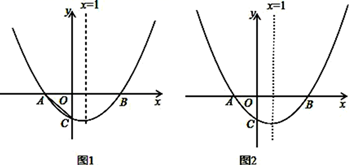    (1)、求出抛物线的解析式及A，B两点的坐标；
    (2)、在对称轴上方是否存在点D，使三角形ADC的周长最小？若存在，求出点D的坐标；若不存在.说明理由（使用图1）；
    (3)、点Q在y轴上，点P在抛物线上，要使Q、P、A. B为顶点的四边形是平行四边形，请求出所有满足条件的点P的坐标（使用图2）.

    查看试题解析