河南省洛阳市偃师市2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-17 类型:期中考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 已知 是正整数, 是整数,则 的值可以是( )A、5 B、7 C、9 D、103. 与根式 的值相等的是( )A、 B、 C、 D、4. 一元二次方程x(x﹣2)=x﹣2的解是( )A、x1=x2=0 B、x1=x2=1 C、x1=0,x2=2 D、x1=1,x2=25. 设方程 的两个根为α,β,那么 的值等于( )A、﹣3 B、﹣1 C、1 D、36. 某商品经过连续两次降价,售价由原来的每件100元降到每件64元,则平均每次降价的百分率为( )A、15% B、40% C、25% D、20%7. 已知a,b,c满足 ,则 的值为( )A、 B、 C、1 D、28. 如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2 , 周长分别是C1与C2 , 则下列说法正确的是( )
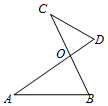 A、 B、 C、 D、9. 如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的周长之比为1:2,点C的坐标为(﹣2,0),若点A的坐标为(﹣4,3),则点E的坐标为( )
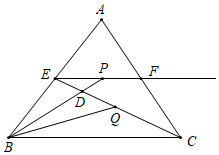
A、 B、 C、 D、9. 如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的周长之比为1:2,点C的坐标为(﹣2,0),若点A的坐标为(﹣4,3),则点E的坐标为( )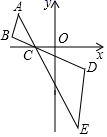 A、( ,﹣6) B、(4,﹣6) C、(2,﹣6) D、10. 如图,函数 的图象经过 斜边 的中点 ,与直角边 相交于 ,连结 .若 ,则 的周长为( )
A、( ,﹣6) B、(4,﹣6) C、(2,﹣6) D、10. 如图,函数 的图象经过 斜边 的中点 ,与直角边 相交于 ,连结 .若 ,则 的周长为( ) A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
11. 若 =6﹣a,则a的取值范围是.12. 若两个最简二次根式 和 是同类二次根式,则n=.13. 若m是一元二次方程x2﹣3x+1=0的一个根,则2020﹣m2+3m=.14. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=7,BC=10,则EF的长为.
 15. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一个根为另一个根的 ,则称这样的方程为“半根方程”.例如方程x2﹣6x+8=0的根为的x1=2,x2=4,则x1= x2 , 则称方程x2﹣6x+8=0为“半根方程”.若方程ax2+bx+c=0是“半根方程”,且点P(a,b)是函数y= x图象上的一动点,则 的值为.
15. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,其中一个根为另一个根的 ,则称这样的方程为“半根方程”.例如方程x2﹣6x+8=0的根为的x1=2,x2=4,则x1= x2 , 则称方程x2﹣6x+8=0为“半根方程”.若方程ax2+bx+c=0是“半根方程”,且点P(a,b)是函数y= x图象上的一动点,则 的值为.三、解答题
-
16. 计算或解方程.(1)、(4 3 ) 2(2)、x2﹣2x﹣5=017. 求代数式a+ 的值,其中a=﹣2020.如图是小亮和小芳的解答过程.
 (1)、的解法是错误的;(2)、错误的原因在于未能正确地运用二次根式的性质:;(3)、求代数式a+2 的值,其中a=﹣2019.18. △ABC在边长为1的正方形网格中如图所示.
(1)、的解法是错误的;(2)、错误的原因在于未能正确地运用二次根式的性质:;(3)、求代数式a+2 的值,其中a=﹣2019.18. △ABC在边长为1的正方形网格中如图所示.
( 1 )以点C为位似中心,作出△ABC的位似图形△A1B1C1 , 使其位似比为1:2.且△A1B1C1位于点C的异侧,并表示出A1的坐标.
( 2 )作出△ABC绕点C顺时针旋转90°后的图形△A2B2C2.
19. 已知 为实数,关于 的方程为 ,(1)、试判断这个方程根的情况;(2)、是否存在实数 ,使这个方程两个根为连续偶数?若存在,求出 及方程的根若不存在,请说明理由.20. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其他两位成员交流的情况.小张:“该商品的进价为24元/件.”
成员甲:“当定价为40元/件时,每天可售出480件.”
成员乙:“若单价每涨1元,则每天少售出20件;若单价每降1元,则每天多售出40件.”根据他们的对话,请你求出要使该商品每天获利7680元,应该怎样合理定价?
21. 小明根据学习函数的经验,对函数y=x+ 的图象与性质进行了探究.下面是小明的探究过程,请补充完整: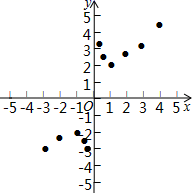 (1)、函数y=x+ 的自变量x的取值范围是.(2)、如表列出了y与x的几组对应值,请写出m,n的值:m= , n=.(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.(4)、结合函数的图象,请完成:
(1)、函数y=x+ 的自变量x的取值范围是.(2)、如表列出了y与x的几组对应值,请写出m,n的值:m= , n=.(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.(4)、结合函数的图象,请完成:①当y= 时,x=;
②写出该函数的一条性质;
③若方程x+ =t有两个相等的实数根,则t的值是.
x
…
﹣3
﹣2
﹣1
1
2
3
4
…
y
…
﹣2
m
2
n
…