重庆市璧山区八校2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-12-17 类型:期中考试
一、单选题
-
1. 在以下回收、绿色食品、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算错误的是( )A、 B、 C、 D、3. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、104. 如图,已知 ,再添加一个条件仍不能判定 的是( )
2. 下列计算错误的是( )A、 B、 C、 D、3. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、104. 如图,已知 ,再添加一个条件仍不能判定 的是( ) A、 B、 C、 D、5. 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A、 B、 C、 D、5. 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( ) A、AAS B、SAS C、ASA D、SSS6. 下列命题中,错误的是( )A、线段的两个端点关于它的垂直平分线对称; B、斜边和一条直角边分别对应相等的两个直角三角形全等; C、等腰三角形的角平分线、中线、高线互相重合; D、五边形共有5条对角线.7. 在下列条件中,能确定 是直角三角形的条件有( )A、 B、 C、 D、8. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )
A、AAS B、SAS C、ASA D、SSS6. 下列命题中,错误的是( )A、线段的两个端点关于它的垂直平分线对称; B、斜边和一条直角边分别对应相等的两个直角三角形全等; C、等腰三角形的角平分线、中线、高线互相重合; D、五边形共有5条对角线.7. 在下列条件中,能确定 是直角三角形的条件有( )A、 B、 C、 D、8. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )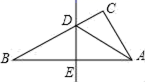 A、10cm B、12cm C、15cm D、17cm9. 如图,多边形 中, , ,则 的值为( )
A、10cm B、12cm C、15cm D、17cm9. 如图,多边形 中, , ,则 的值为( )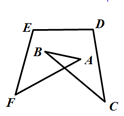 A、84° B、80° C、72° D、60°10. 如图,在 中, 与 关于直线EF对称, ,连接 ,则 的度数是( )
A、84° B、80° C、72° D、60°10. 如图,在 中, 与 关于直线EF对称, ,连接 ,则 的度数是( ) A、20° B、30° C、40° D、50°11. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
A、20° B、30° C、40° D、50°11. 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )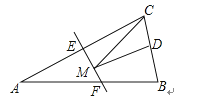 A、6 B、8 C、10 D、1212. 如图 是长方形纸带, ,将纸带沿 折叠成图 ,再沿 折叠成图 ,则图 中的 的度数是( )
A、6 B、8 C、10 D、1212. 如图 是长方形纸带, ,将纸带沿 折叠成图 ,再沿 折叠成图 ,则图 中的 的度数是( ) A、102° B、112° C、120° D、128°
A、102° B、112° C、120° D、128°二、填空题
-
13. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是.14. 若 ,则 的值是.15. 如图, 是 的中线, 是 的中线, 是 的中线,若 的面积为1 cm 2 , 则 的面积为cm 2.
 16. 如图, ,点P是 平分线上的一点, 于D, 交 于E,已知 ,则 .
16. 如图, ,点P是 平分线上的一点, 于D, 交 于E,已知 ,则 . 17. 如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为
17. 如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为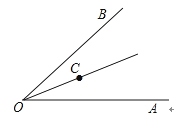 18. 如图,已知: ,点 、 、 在射线 上,点 、 、 在射线 上,△ 、△ 、△ 均为等边三角形,若 ,则△ 的边长为 .
18. 如图,已知: ,点 、 、 在射线 上,点 、 、 在射线 上,△ 、△ 、△ 均为等边三角形,若 ,则△ 的边长为 .
三、解答题
-
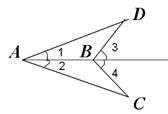
19. 计算:(1)、 ;(2)、 .20. 已知:∠1=∠2,∠3=∠4.求证:AC=AD
 21. 如图所示,在平面直角坐标系中,△ABC各顶点的坐标分别为A(4,0),B(-1,4),C(-3,1).
21. 如图所示,在平面直角坐标系中,△ABC各顶点的坐标分别为A(4,0),B(-1,4),C(-3,1). (1)、作出△A′B′C′,使△A′B′C′和△ABC关于x轴对称;(2)、写出点A′, B′,C′的坐标;(3)、求△ABC的面积.22. 用一条长为30的绳子围成一个等腰三角形.(1)、若腰长是底长的2倍,那么各边长是多少?(2)、若等腰三角形有一条边长为7,它的其它两边是多少?23. 如图,已知,在 中, , 平分 ,点 是线段 (除去端点 )上一动点, 于点 .
(1)、作出△A′B′C′,使△A′B′C′和△ABC关于x轴对称;(2)、写出点A′, B′,C′的坐标;(3)、求△ABC的面积.22. 用一条长为30的绳子围成一个等腰三角形.(1)、若腰长是底长的2倍,那么各边长是多少?(2)、若等腰三角形有一条边长为7,它的其它两边是多少?23. 如图,已知,在 中, , 平分 ,点 是线段 (除去端点 )上一动点, 于点 . (1)、若 , ,求 的度数.(2)、若 , ,请用含 的式子表示 的度数.24. 如图,点 是等边 内一点, , .以 为一边作等边 ,连接 .
(1)、若 , ,求 的度数.(2)、若 , ,请用含 的式子表示 的度数.24. 如图,点 是等边 内一点, , .以 为一边作等边 ,连接 . (1)、求证: ;(2)、当 时,试判断 的形状,并说明理由.25. 对每个数位数字均不为零且互不相等的一个三位正整数 ,若将 的十位数字与百位数字交换位置,得到一个新的三位数 ,我们称 为 的“置换数”,如:123的“置效为“213”;若由 的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为 ,我们称 为 的“行生数”.如456:因为 所以 的“衍生数”为330.(1)、直接写出987的“置换数”,并求987的“衍生数”;(2)、对每个数位数字均不为零且互不相等的一个三位正整数 ,设十位数字为 ,若 的“衍生数”与 的“置换数”之差为102,求 .26. 如图
(1)、求证: ;(2)、当 时,试判断 的形状,并说明理由.25. 对每个数位数字均不为零且互不相等的一个三位正整数 ,若将 的十位数字与百位数字交换位置,得到一个新的三位数 ,我们称 为 的“置换数”,如:123的“置效为“213”;若由 的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为 ,我们称 为 的“行生数”.如456:因为 所以 的“衍生数”为330.(1)、直接写出987的“置换数”,并求987的“衍生数”;(2)、对每个数位数字均不为零且互不相等的一个三位正整数 ,设十位数字为 ,若 的“衍生数”与 的“置换数”之差为102,求 .26. 如图 (1)、如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;(2)、如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.(3)、如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE=.(不需证明)
(1)、如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;(2)、如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.(3)、如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE=.(不需证明)