湖北省十堰市房县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个应用图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以长度为下列各组数据的线段为边，能构成三角形的是（）

A、 $3 c m ， 4 c m ， 8 c m$ B、 $5 c m ， 6 c m ， 10 c m$ C、 $7 c m ， 8 c m ， 15 c m$ D、 $6 c m ， 3 c m ， 3 c m$

查看试题解析
3. 计算 ${(a b^{3})}^{2}$ 的结果是（）

A、 $2 a b^{3}$ B、 $a b^{6}$ C、 $a^{2} b^{5}$ D、 $a^{2} b^{6}$

查看试题解析
4. 等腰三角形有一个角是90°，则另两个角分别是（）

A、30°，60° B、45°，45° C、45°，90° D、20°，70°

查看试题解析
5. 下列计算正确的是 $($ $)$

A、 $a^{3} + a^{3} = 2 a^{3}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(a^{3})}^{2} = a^{5}$

查看试题解析
6. 已知一个多边形的内角和是540 $°$ ，则这个多边形的对角线条数是（）

A、5 B、7 C、9 D、10

查看试题解析
7. 下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）

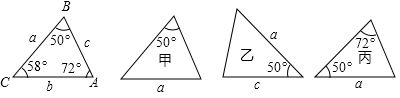A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙

查看试题解析
8. 若 $x + y = 1$ 且 $x y = - 2$ ，则代数式 $(1 - x) (1 - y)$ 的值等于（）

A、-2 B、0 C、1 D、2

查看试题解析
9. 点 $(2, 5)$ 关于直线 $x = 1$ 对称的点的坐标为（）

A、 $(- 2, 5)$ B、 $(- 3, 5)$ C、 $(4, 5)$ D、 $(0, 5)$

查看试题解析
10. 已知，如图，等腰△ABC，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下列结论：①AC平分∠PAD；②∠APO＝∠DCO；③△OPC是等边三角形；④AC＝AO+AP；其中正确的序号是（）

A、①③④ B、②③ C、①②④ D、①③

查看试题解析

二、填空题

11. 内角和与外角和相等的多边形的边数是.

查看试题解析
12. 我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k＝ $\frac{1}{4}$ ，则该等腰三角形的顶角为．

查看试题解析
13. 计算： $- {(m^{3})}^{2} \div m^{4} =$ .

查看试题解析
14. 在平面直角坐标系中，点 $M (a ， b)$ 与点 $N (3 ， - 1)$ 关于 $x$ 轴对称，则 $a + b$ 的值是．

查看试题解析
15. 如图，△ABC纸片中，AB=AC，∠BAC＝90°，BC＝8，沿过点C的直线折叠这个三角形，使点A落在BC边上的点F处，折痕为CD，BE⊥CD，垂足E在CD的延长线上，则结论①DF=DA；②∠ABE＝22.5 $°$ ；③△BDF 的周长为8；④CD=2BE.正确的是（填上正确的结论序号）.

查看试题解析

三、解答题

16. 计算： $| - 2 | - \sqrt{9} - \frac{1}{2} \times 4 - {(\sqrt{3} - 2)}^{0}$

查看试题解析
17. 已知 $x^{2} + p x + 8$ 与 $x^{2} - 3 x + q$ 的乘积中不含 $x^{3}$ 和 $x^{2}$ 项，求 $p, q$ 的值.

查看试题解析
18. 如图，已知 AB=AC，∠A=40^° ， AB=10，DC=3，AB 的垂直平分线 MN 交 AC 于点 D，求∠DBC 的度数、线段 BD 的长度。

查看试题解析
19. 如图，平面直角坐标系中，A(－2，1)，B(－3，4)，C(－1，3)，过点(l，0)作x轴的垂线 $l$ .

(1)、作出△ABC关于直线 $l$ 的轴对称图形△ $A^{'} B^{'} C^{'}$ ；

(2)、直接写出A₁( ， )，B₁( ， )，C₁( ， )；

(3)、在△ABC内有一点P(m，n)，则点P关于直线 $l$ 的对称点P₁的坐标为( ， )(结果用含m，n的式子表示).

查看试题解析
20. 已知△ABN和△ACM位置如图所示，AB＝AC，AD＝AE，∠1＝∠2.

求证：

(1)、BD＝CE；

(2)、∠M＝∠N.

查看试题解析
21. 如图，某市有一块长为（2a+b）米，宽为（a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像.

(1)、试用含a，b的代数式表示绿化的面积是多少平方米？

(2)、若a＝3，b＝2，请求出绿化面积.

查看试题解析
22. 小马、小虎两人共同计算一道题：（x+a）（2x+b）.由于小马抄错了a的符号，得到的结果是2x²﹣7x+3，小虎漏抄了第二个多项式中x的系数得到的结果是x²+2x﹣3.

(1)、求a，b的值；

(2)、细心的你请计算这道题的正确结果；

(3)、当x＝﹣1时，计算（2）中的代数式的值.

查看试题解析
23. 已知，如图，△ABC为等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1．

(1)、求证：△ABE≌△CAD；

(2)、求∠BPQ的度数；

(3)、求AD的长．

查看试题解析
24. 如图1，在平面直角坐标系中，直线AB与x轴交于点A（m，0），与y轴交于点B（0，n），且m，n满足：（m＋n ）²＋|n－6| ＝0.

(1)、求：①m，n的值；② S_△_ABE的值；

(2)、D为OA延长线上一动点，以BD为直角边作等腰直角△BDE，连接EA，求直线EA与y轴交点F的坐标.

(3)、如图2，点E为y轴正半轴上一点，且 ∠OAE＝ 30°，AF平分∠OAE，点M是射线AF上一动点，点N是线段OA上一动点，试求OM＋MN 的最小值（图1与图2中点A的坐标相同）.

查看试题解析