河南省濮阳市台前县2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2020-12-17 类型：期中考试
一、单选题
-
1. 2020年的春节，对于所有人来说真的不一般.为了打好疫情攻坚战，医护人员在岗位上同时间赛跑，与病魔较量，而我们每个人都能为打赢这场仗贡献一份力量.勤洗手，戴口罩，少聚会，积极配合；防控工作，照顾好自己和家人，还有，说出一句简单的：中国加油.武汉加油.在“中国加油”这4个汉字中，不可以看作轴对称图形的个数为（ ）A、 1 B、2 C、3 D、42. 下列长度的三条线段，能组成三角形的是（ ）A、3，4，8 B、5，6，10 C、5，5，11 D、5，6，113. 下列叙述中错误的一项是（ ）A、三角形的中线、角平分线、高都是线段 B、三角形的三条高线中至少存在一条在三角形内部 C、只有一条高在三角形内部的三角形一定是钝角三角形 D、三角形的三条角平分线都在三角形内部4.
将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上，则∠1的度数为（ ）
A、75° B、65° C、45° D、30°5. 已知等腰三角形的周长为17cm，一边长为4cm，则它的腰长为（ ）A、4cm B、6.5cm或9cm C、6.5cm D、4cm或6.5cm6. 如图，三角形纸片ABC，AB＝10cm，BC＝7cm，AC＝6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（ ）
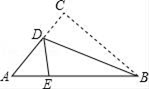A、9cm B、13cm C、16cm D、10cm7. 如图所示，已知∠1=∠2，下列添加的条件不能使△ADC≌△CBA的是（ ）
A、 B、 C、 D、8. 如图，等边△ABC的边长为4，AD是边BC上的中线，F是边AD上的动点，E是边AC上一点，若AE=2，则EF+CF取得最小值时，∠ECF的度数为（ ）
A、15° B、22.5° C、30° D、45°9. 如图，已知△ABC和△CDE都是等边三角形，且A、C、E三点共线.AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：① AD=BE；② ∠AOB=60°；③AP=BQ； ④△PCQ是等边三角形；⑤PQ∥AE.其中正确结论的有（ ）个
A、5 B、4 C、3 D、210. 如图，在 中，点 是边 、 的垂直平分线的交点，已知 ，则 （ ）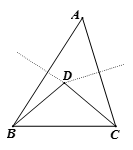
A、 B、 C、 D、二、填空题
-
11. 一个正多边形的每个外角为60°，那么这个正多边形的内角和是。12. 若点M（﹣3，a）与点N（b，4）关于x轴对称，则a+b＝.13. 我们规定：等腰三角形的顶角与一个底角度数的比值叫作等腰三角形的“特征值”，记作k．若 ，则该等腰三角形的顶角为度．14. 如图，在直角坐标系中，AD是Rt△OAB的角平分线，已知点D的坐标是（0，﹣4），AB的长是12，则△ABD的面积为 ．
15. 有一张三角形纸片ABC ， ∠A＝80°，点D是AC边上一点，沿BD方向剪开三角形纸片后，发现所得两张纸片均为等腰三角形，则∠C的度数可以是 ．三、解答题
-
16. 如图，学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”，按照设计要求，英语角C到两栋教学楼A，B的距离必须相等，到两条小路的距离也必须相等，则“英语角”应修建在什么位置？请在图上标出它的位置.（尺规作图，不写作法，保留作图痕迹）
17. 已知：如图，E、C是BF上两点，且AB∥DE，BE＝FC，∠A＝∠D.求证：AC＝DF.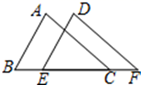
18. 如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣3），C（﹣1，﹣1）．
(1)、在图中作出△ABC关于y轴对称的△A1B1C1；(2)、写出点△A1 ， B1 ， C1的坐标（直接写答案）：A1；B1；C1；(3)、△A1B1C1的面积为；(4)、在y轴上画出点P，使PB+PC最小．19. 如图，在△ABC中，D是BC边上的一点，AB＝DB，BE平分∠ABC，交AC边于点E，连接DE.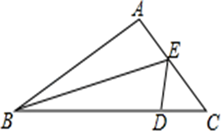
(1)、求证：△ABE≌△DBE；(2)、若∠A＝100°，∠C＝50°，求∠AEB的度数.20. 如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，连接CD，交BE于点F.求证：BE垂直平分CD.
21. 如图，在等边△ABC中，点D为BC边上的一点，在等边△ABC的外角平分线CE上取一点E，使CE＝BD，连接AE、DE，请判断△ADE的形状，并说明理由.
22. 已知，△ABC是等腰直角三角形，BC=AB，A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方．
(1)、如图1所示，若A的坐标是（﹣3，0），点B的坐标是（0，1），求点C的坐标；(2)、如图2，过点C作CD⊥y轴于D，请直接写出线段OA，OD，CD之间等量关系；(3)、如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F，问CF与AE有怎样的数量关系？并说明理由．23. 如图，在△ABC中，AB=AC=12cm，BC=9cm，点D为AB的中点.
(1)、如果点P在线段BC上以3厘米/秒的速度由B向C点运动，同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等，当经过1秒时，△BPD与△CQP是否全等，请判断并说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CPQ？
(2)、若点Q以②的运动速度从点C出发，点P以原来运动速度从点B同时出发，都逆时针沿△ABC的三边运动，求经过多长时间，点P与点Q第一次在△ABC的哪条边上会相遇？