河南省信阳市罗山县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-17 类型:期末考试
一、单选题
-
1. 下列全国志愿者服务标识的设计图中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算 的结果为( )
2. 计算 的结果为( )
A、 B、 C、 D、3. 若分式 的值为零,则x的值是( )A、3 B、-3 C、±3 D、04. 化简 的结果为( )A、 B、a﹣1 C、a D、15. 下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )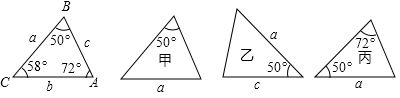 A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙6. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则BC的长是( )
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙6. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则BC的长是( ) A、 B、2 C、 D、8. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A、 B、2 C、 D、8. 如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )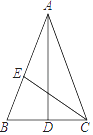 A、20° B、35° C、40° D、70°9. 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,这样剪得的△ADH中 ( )
A、20° B、35° C、40° D、70°9. 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,这样剪得的△ADH中 ( ) A、AH=DH≠AD B、AH=DH=AD C、AH=AD≠DH D、AH≠DH≠AD10. 如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
A、AH=DH≠AD B、AH=DH=AD C、AH=AD≠DH D、AH≠DH≠AD10. 如图,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( ) A、∠1=∠EFD B、BE=EC C、BF=DF=CD D、FD∥BC
A、∠1=∠EFD B、BE=EC C、BF=DF=CD D、FD∥BC二、填空题
-
11. 分解因式:2x3﹣6x2+4x= .12. 若A(2,b),B(a,-3)两点关于y轴对称,则a-b=.13. 如图,七边形ABCDEFG中,AB,ED的延长线交于点O,外角∠1,∠2,∠3,∠4的和等于220°,则∠BOD的度数是度.
 14. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB=。
14. 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB=。 15. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙 若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为.
15. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙 若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为.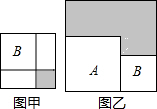
三、解答题
-
16. 先化简,再求值: ,其中 .17. 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
 (1)、求出 的面积;(2)、在图中作出 关于y轴的对称图形 ;(3)、直接写出点 的坐标.18. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)、求出 的面积;(2)、在图中作出 关于y轴的对称图形 ;(3)、直接写出点 的坐标.18. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
 (1)、求∠CBE的度数;
(1)、求∠CBE的度数;
(2)、过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
19. 如图(单位:m),某市有一块长为(3a+b)m、宽为(2a+b)m的长方形地,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=6,b=1时,绿化的面积.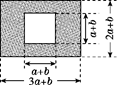 20. 中, , ,AC的垂直平分线交AB于E,D为垂足,连结EC.
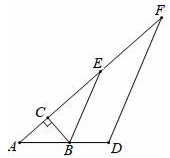
20. 中, , ,AC的垂直平分线交AB于E,D为垂足,连结EC. (1)、求 的度数;(2)、若 ,求 长.21. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D.
(1)、求 的度数;(2)、若 ,求 长.21. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D. (1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.22. 2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.22. 2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)、求甲、乙两种货车每辆车可装多少件帐篷;(2)、如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.23. 如图,在长方形ABCD中,AB=CD=6cm , BC=10cm , 点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒: (1)、PC=cm . (用t的代数式表示)(2)、当t为何值时,△ABP≌△DCP?(3)、当点P从点B开始运动,同时,点Q从点C出发,以vcm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
(1)、PC=cm . (用t的代数式表示)(2)、当t为何值时,△ABP≌△DCP?(3)、当点P从点B开始运动,同时,点Q从点C出发,以vcm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.