河南省舞钢市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-17 类型:期末考试
一、单选题
-
1. 下列方程中是二元一次方程的是( )A、 B、 C、 D、2. 方程组 的解是( )A、 B、 C、 D、3. 下列说法中正确的是( )A、 的值是±5 B、两个无理数的和仍是无理数 C、-3没有立方根. D、 是最简二次根式.4. 线段CD是由线段AB平移得到的,点A(3,-1)的对应点C的坐标是(-2,5),则点B(0,4)的对应点D的坐标是( ).A、(5,-7) B、(4,3) C、(-5,10) D、(-3,7)5. 下列命题中的假命题是( )A、三角形的一个外角大于内角 B、同旁内角互补,两直线平行 C、 是二元一次方程 的一个解 D、方差是刻画数据离散程度的量6. 已知:一组数据-1,2,-1,5,3,4,关于这组数据,下列说法错误的是( )A、平均数是2 B、众数和中位数分别是-1和2.5 C、方差是16 D、标准差是7. 如图,△ABC中,AB=10,BC=12,AC= ,则△ABC的面积是( ).
 A、36 B、 C、60 D、8. 已知:一次函数 的图象经过点A( ,1)和点B( ,-3)且 < ,则它的图象大致是( ).A、
A、36 B、 C、60 D、8. 已知:一次函数 的图象经过点A( ,1)和点B( ,-3)且 < ,则它的图象大致是( ).A、 B、
B、 C、
C、 D、
D、 9. 如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )
9. 如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是( )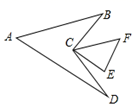 A、40° B、45° C、50° D、60°10. 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A、40° B、45° C、50° D、60°10. 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
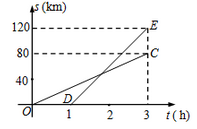 A、
A、 B、
B、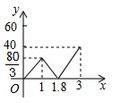 C、
C、 D、
D、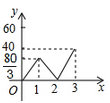
二、填空题
-
11. 如图,点A的坐标(-2,3)点B的坐标是(3,-2),则图中点C的坐标是.
 12. 一次函数 ( , , 是常数)的图象如图所示.则关于x的方程 的解是.
12. 一次函数 ( , , 是常数)的图象如图所示.则关于x的方程 的解是. 13. 一个大型商场某天销售的某品牌的运动鞋的数量和尺码如下表:
13. 一个大型商场某天销售的某品牌的运动鞋的数量和尺码如下表:鞋的尺码(单位:厘米)
22.5
23
24
24.5
25
销售量(单位:双)
2
4
3
1
2
这些鞋的尺码组成的一组数据的中位数是.
14. 如图,四边形ABCD中,∠A=90°,AB=2,AD= ,CD=3,BC=5,则四边形ABCD的面积是. 15. 的平方根是±3, 的立方根是2,则 的值是.16. 在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组.
15. 的平方根是±3, 的立方根是2,则 的值是.16. 在如图所示的长方形中放置了8个大小和形状完全相同的小长方形,设每个小长方形的长为x,宽为y,根据图中提供的数据,列方程组. 17. 如图,直线AB∥CD,直线EF分别与直线AB和直线CD交于点E和F,点P是射线EA上的一个动点(P不与E重合)把△EPF沿PF折叠,顶点E落在点Q处,若∠PEF=60°,且∠CFQ:∠QFP=2:5,则∠PFE的度数是.
17. 如图,直线AB∥CD,直线EF分别与直线AB和直线CD交于点E和F,点P是射线EA上的一个动点(P不与E重合)把△EPF沿PF折叠,顶点E落在点Q处,若∠PEF=60°,且∠CFQ:∠QFP=2:5,则∠PFE的度数是. 18. 为了提高居民的节水意识,今年调整水价,不仅提高了每立方的水价,还施行阶梯水价.图中的 和 分别表示去年和今年的水费 (元)和用水量 ( )之间的函数关系图象.如果小明家今年和去年都是用水150 ,要比去年多交水费元.
18. 为了提高居民的节水意识,今年调整水价,不仅提高了每立方的水价,还施行阶梯水价.图中的 和 分别表示去年和今年的水费 (元)和用水量 ( )之间的函数关系图象.如果小明家今年和去年都是用水150 ,要比去年多交水费元.
三、解答题
-
19. 计算及解方程组:(1)、(2)、(3)、解方程组:20. 在如图所示的平面直角坐标系中,描出点A(3,2)和点B(-1,4).
 (1)、求点A(3,2)关于x轴的对称点C的坐标;(2)、计算线段BC的长度.21. 某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:
(1)、求点A(3,2)关于x轴的对称点C的坐标;(2)、计算线段BC的长度.21. 某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:甲:8,8,7,8,9;乙:5,9,7,10,9;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
a
9
c
3.2
根据以上信息,回答下列问题:
(1)、表格是a= , b= , c=.(填数值)(2)、体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是;(3)、如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数 , 中位数 , 方差.(填“变大”、“变小”或“不变”)22. 如图,△ABC中,AD是角平分线,点G在CA的延长线上,GE交AB于F,交BC于点E,并且∠G=∠AFG.求证:AD∥EF.
 23. 工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
23. 工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.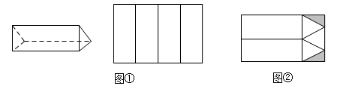 (1)、若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?(2)、一共能生产多少个巧克力包装盒?24. 甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示.
(1)、若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?(2)、一共能生产多少个巧克力包装盒?24. 甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y(千米)与甲出发时间x(小时)的函数关系如图所示. (1)、点A的实际意义是什么?(2)、求甲、乙两人的速度;(3)、求OC和BD的函数关系式;(4)、求学校和博物馆之间的距离.
(1)、点A的实际意义是什么?(2)、求甲、乙两人的速度;(3)、求OC和BD的函数关系式;(4)、求学校和博物馆之间的距离.