河南省三门峡市渑池县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-17 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下面四个图形中,属于轴对称图形的是( )A、
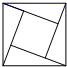 B、
B、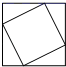 C、
C、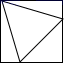 D、
D、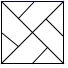 3. 下列各式中,正确的是( )A、 B、 C、 =b+1 D、 =a+b4. 如图,在 中, 过点 作 于 , 则 的长是( )
3. 下列各式中,正确的是( )A、 B、 C、 =b+1 D、 =a+b4. 如图,在 中, 过点 作 于 , 则 的长是( ) A、 B、 C、 D、5. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A、 B、 C、 D、5. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确6. 若要使等式 成立,则 等于( )A、 B、 C、 D、7. 下列三角形中:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有( )A、①②③ B、①②④ C、①③④ D、①②③④8. 若分式 的值为 则( )A、 B、 C、 或 D、 或9. 如图,在钝角三角形 中, 为钝角,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧;两弧交于点 连结 的延长线交 于点 .下列结论: 垂直平分 ; 平分 ; 是等腰三角形; 是等边三角形.其中正确的有( )
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确6. 若要使等式 成立,则 等于( )A、 B、 C、 D、7. 下列三角形中:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有( )A、①②③ B、①②④ C、①③④ D、①②③④8. 若分式 的值为 则( )A、 B、 C、 或 D、 或9. 如图,在钝角三角形 中, 为钝角,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧;两弧交于点 连结 的延长线交 于点 .下列结论: 垂直平分 ; 平分 ; 是等腰三角形; 是等边三角形.其中正确的有( ) A、 个 B、 个 C、 个 D、 个10. 如图,在△ABC中,AB=AC,BC=10,S△ABC=60,AD⊥BC于点D,EF垂直平分AB,交AB于点E,AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为( )
A、 个 B、 个 C、 个 D、 个10. 如图,在△ABC中,AB=AC,BC=10,S△ABC=60,AD⊥BC于点D,EF垂直平分AB,交AB于点E,AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为( ) A、10 B、11 C、12 D、13
A、10 B、11 C、12 D、13二、填空题
-
11. 2018年4月18日,被誉为“中国天眼”的FAST望远镜首次发现的毫秒脉冲星得到国际认证.新发现的脉冲星自转周期为0.00519秒,是至今发现的射电流量最弱的高能毫秒脉冲星之一.将0.00519用科学记数法表示应为.12. 我国是一个水资源贫乏的国家,每一个公民都应自觉养成节约用水的意识和习惯,为提高水资源的利用率,某住宅小区安装了循环用水装置.经测算,原来 天用水 吨,现在这些水可多用4天,现在每天比原来少用水吨.13. 如果 那么 .(用含 的式子表示)14. 在RtΔABC中,∠B=90°,∠A=30°,DE垂直平分AC,交AC于点E,交AB于点D,连接CD,若BD=2,则AD的长是.
 15. 若解分式方程 产生增根,则 .
15. 若解分式方程 产生增根,则 .三、解答题
-
16. 因式分解:(1)、 ;(2)、17. 解下列方程.(1)、(2)、18. 先化简 ,再从 中选一个合适的数作为 的值代入求值.19. 为中华人民共和国成立70周年献礼,某灯具厂计划加工6000套彩灯,为尽快完成任务,实际每天加工彩灯的数量是原计划的1.5倍,结果提前5天完成任务.求该灯具厂原计划每天加工这种彩灯的数量.20. 在 中, 垂直平分 ,分别交 、 于点 、 , 垂直平分 ,分别交 , 于点 、 .
 (1)、如图①,若 ,求 的度数;(2)、如图②,若 ,求 的度数;(3)、若 ,直接写出用 表示 大小的代数式.21. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题:
(1)、如图①,若 ,求 的度数;(2)、如图②,若 ,求 的度数;(3)、若 ,直接写出用 表示 大小的代数式.21. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题: (1)、写出图2中所表示的数学等式(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:
(1)、写出图2中所表示的数学等式(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:若 , ,则 .


