河南省洛阳市洛宁县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-12-17 类型：期末考试
一、单选题
-
1. 下列运算正确的是（ ）A、a2+a2=a4 B、（﹣b2）3=﹣b6 C、2x•2x2=2x3 D、（m﹣n）2=m2﹣n22. 一个正数的两个平方根分别是2a-1与-a+2，则a的值为（ ）A、1 B、-1 C、2 D、-23.
如图，在△ABC中，∠C=90°，AB的垂直平分线MN分别交AC，AB于点D，E．若∠CBD：∠DBA=2：1，则∠A为（ ）
A、20° B、25° C、22.5° D、30°4. 如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（ ）
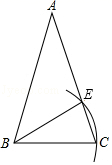A、AE＝EC B、AE＝BE C、∠EBC＝∠BAC D、∠EBC＝∠ABE5. 已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长（ ）A、4 B、16 C、 D、4或6. 如图，在△ABC中，AB=8，BC=10，AC=6，则BC边上的高AD为（ ）
A、8 B、9 C、 D、107. 用反证法证明“在一个三角形中，至少有一个内角小于或等于60°”时应假设（ ）A、三角形中有一个内角小于或等于60° B、三角形中有两个内角小于或等于60° C、三角形中有三个内角小于或等于60° D、三角形中没有一个内角小于或等于60°8.小明家下个月的开支预算如图所示，如果用于衣服上的支是200元，则估计用于食物上的支出是（ ）
A、200元 B、250元 C、300元 D、3509. 一次数学测试后，某班40名学生的成绩被分为5组，第1～4组的频数分别为12、10、6、8，则第5组的频率是（ ）
A、0.1 B、0.2 C、0.3 D、0.410. 如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点B落在点B′处，则重叠部分△AFC的面积为（ ）
A、12 B、10 C、8 D、6二、填空题
-
11. 计算：|-2| =.12. 如图，以数轴的单位长度线段为边做一个正方形以表示数2的点为圈心，正方形对角线长为半径画半圆，交数轴于点A和点B，则点A表示的数是
13. 如图所示，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是.
14. 实数 ， ， ， ， 中，其中无理数出现的频数是.15. 如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则 周长的最小值为.
三、解答题
-
16. 已知2a－1的算术平方根是3，3a＋b－1的平方根是±4，c是 的整数部分，求a＋2b－c的平方根．17. 计算(1)、(2)、18. 如图，△ABC中，AB=BC，∠ABC=45°，BE⊥AC于点E，AD⊥BC于点D，BE与AD相交于F.
(1)、求证：BF=AC；(2)、若CD=1，求AF的长.19. 如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°.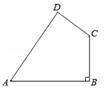
(1)、判断∠D是否是直角，并说明理由.(2)、求四边形ABCD的面积.20.某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．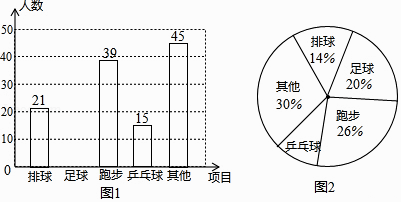
请结合以上信息解答下列问题：
(1)、m=；(2)、请补全上面的条形统计图；(3)、在图2中，“乒乓球”所对应扇形的圆心角的度数为；(4)、已知该校共有1200名学生，请你估计该校约有名学生最喜爱足球活动．21. 如图，一架长25米的梯子，斜靠在竖直的墙上，这时梯子底端离墙7米．
(1)、此时梯子顶端离地面多少米？(2)、若梯子顶端下滑4米，那么梯子底端将向左滑动多少米？22. 为整治城市街道的汽车超速现象，交警大队在某街道旁进行了流动测速.如图，一辆小汽车在某城市街道上直行，某一时刻刚好行驶到离车速检测仪 的 处，过了 后，小汽车到达离车速检测仪 的 处，已知该段城市街道的限速为 ，请问这辆小汽车是否超速？
23. 如图，已知△ABC中，∠B=90°，AB=8，CB=6，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒.
(1)、当t=2秒时，求PQ的长；(2)、求出发时间为几秒时，△PQB是等腰三角形?(3)、若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等 腰三角形的运动时间。