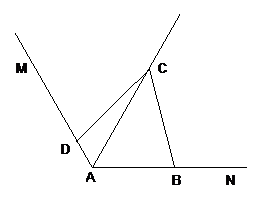河南省安阳市内黄县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-17 类型:期末考试
一、单选题
-
1. 下列手机软件图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米.其中,0.00005用科学记数法表示为( )A、0.5×10﹣4 B、5×10﹣4 C、5×10﹣5 D、50×10﹣33. 下列长度的三条线段可以组成三角形的是( )A、3,4,2 B、12,5,6 C、1,5,9 D、5,2,74. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )
2. 叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米.其中,0.00005用科学记数法表示为( )A、0.5×10﹣4 B、5×10﹣4 C、5×10﹣5 D、50×10﹣33. 下列长度的三条线段可以组成三角形的是( )A、3,4,2 B、12,5,6 C、1,5,9 D、5,2,74. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )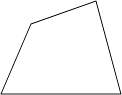 A、0根 B、1根 C、2根 D、3根5. 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
A、0根 B、1根 C、2根 D、3根5. 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( ) A、82° B、72° C、60° D、36°6. 若关于 的方程 的解为正数,则 的取值范围是( )A、 B、 C、 且 D、 且7. 若 ,则 的值为( )A、3 B、6 C、9 D、128. 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )
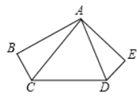
A、82° B、72° C、60° D、36°6. 若关于 的方程 的解为正数,则 的取值范围是( )A、 B、 C、 且 D、 且7. 若 ,则 的值为( )A、3 B、6 C、9 D、128. 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )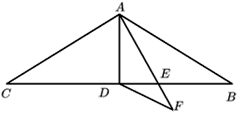 A、4.5 B、5 C、5.5 D、69. 如图的七边形ABCDEFG中,AB,ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A、4.5 B、5 C、5.5 D、69. 如图的七边形ABCDEFG中,AB,ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )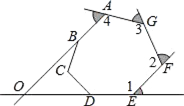 A、40° B、45° C、50° D、60°10. 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
A、40° B、45° C、50° D、60°10. 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )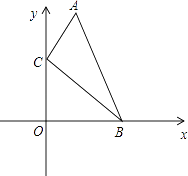 A、(0,0) B、(0,1) C、(0,2) D、(0,3)
A、(0,0) B、(0,1) C、(0,2) D、(0,3)二、填空题
-
11. 如图:已知AB⊥BC,AE⊥DE,且AB=AE,∠ACD=∠ADC=50°,∠BAD=100°,则∠BAE= .
 12. 已知等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的顶角度数为.13. 如果实数 x,y 满足方程组 ,那么代数式( +2)÷ 的值为 .14. 一个正多边形的每个内角都比与它相邻的外角的3倍还多20°,则此正多边形是 边形,共有 条对角线.15. 分解因式:(1)、3a2-6a+3=;(2)x2+7x+10 = .
12. 已知等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的顶角度数为.13. 如果实数 x,y 满足方程组 ,那么代数式( +2)÷ 的值为 .14. 一个正多边形的每个内角都比与它相邻的外角的3倍还多20°,则此正多边形是 边形,共有 条对角线.15. 分解因式:(1)、3a2-6a+3=;(2)x2+7x+10 = .三、解答题
-
16. 计算(1)、[2a(a2b-ab2)+ab(ab-a2)] ÷a2b(2)、 ÷17. 解方程: .18. 先化简,再求值: ,其中 , .19. 如图,在△ABC中,∠BAC=50°,∠C=60°,AD⊥BC,
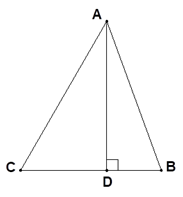 (1)、用尺规作图作∠ABC的平分线BE,且交AC于点E,交AD于点F(不写作法,保留作图痕迹);(2)、求∠BFD的度数.20. 已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴.
(1)、用尺规作图作∠ABC的平分线BE,且交AC于点E,交AD于点F(不写作法,保留作图痕迹);(2)、求∠BFD的度数.20. 已知:如图,在△ABC中,点A的坐标为(﹣4,3),点B的坐标为(﹣3,1),BC=2,BC∥x轴. (1)、画出△ABC关于y轴对称的图形△A1B1C1;并写出A1 , B1 , C1的坐标;(2)、求以点A、B、B1、A1为顶点的四边形的面积.21. 为了在学生中倡导扶危救困的良好社会风尚,营造和谐文明进步的校园环境,某校举行了 “爱心永恒,情暖校园”慈善一日捐活动,在本次活动中,某同学对甲.乙两班捐款的情况进行统计,得到如下三条信息:
(1)、画出△ABC关于y轴对称的图形△A1B1C1;并写出A1 , B1 , C1的坐标;(2)、求以点A、B、B1、A1为顶点的四边形的面积.21. 为了在学生中倡导扶危救困的良好社会风尚,营造和谐文明进步的校园环境,某校举行了 “爱心永恒,情暖校园”慈善一日捐活动,在本次活动中,某同学对甲.乙两班捐款的情况进行统计,得到如下三条信息:信息一 甲班共捐款120元,乙班共捐款88元;
信息二 乙班平均每人捐款数比甲班平均每人捐款数的0.8倍;
信息三 甲班比乙班多5人.
请你根据以上三条信息,求出甲班平均每人捐款多少元?
22. 如图1,△ABC为等边三角形,点E、F分别在BC和AB上,且CE=BF,AE与CF相交于点H.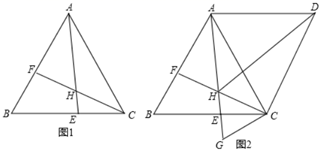 (1)、求证:△ACE≌△CBF;(2)、求∠CHE的度数;(3)、如图2,在图1上以AC为边长再作等边△ACD,将HE延长至G使得HG=CH,连接HD与CG,求证:HD=AH+CH23.(1)、如图中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC=BC; ②AD+AB=AC.请你证明结论②;
(1)、求证:△ACE≌△CBF;(2)、求∠CHE的度数;(3)、如图2,在图1上以AC为边长再作等边△ACD,将HE延长至G使得HG=CH,连接HD与CG,求证:HD=AH+CH23.(1)、如图中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC=BC; ②AD+AB=AC.请你证明结论②; (2)、如图中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(2)、如图中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.