初中数学北师大版八年级上学期期末考试复习专题:11 三角形的内角和定理
试卷更新日期:2020-12-17 类型:复习试卷
一、单选题
-
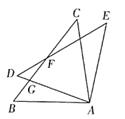
1. 如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
 A、15° B、20° C、25° D、30°2. 一个三角形三个内角的度数之比是3:4:5,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 等腰 中, ,若 ,则 的度数是( )A、 B、 C、 D、4. 下列说法中,正确的有( )
A、15° B、20° C、25° D、30°2. 一个三角形三个内角的度数之比是3:4:5,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 等腰 中, ,若 ,则 的度数是( )A、 B、 C、 D、4. 下列说法中,正确的有( )①如果 ,那么 是直角三角形;②如果 ,则 是直角三角形;③如果三角形三边之比为 ,则 为直角三角形;④如果三角形三边长分别是 、 、 ,则 是直角三角形.
A、1个 B、2个 C、3个 D、4个5. 若 的三边长分别是 , , ,则下列条件:
(1) ;(2) ;(3) ;(4)其中能判定 是直角三角形的个数有( ).
A、4个 B、3个 C、2个 D、1个二、填空题
-
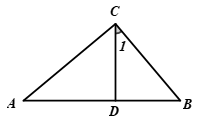
6. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,如果∠A=40°,则∠1=度.
 7. 在△ABC中,已知∠A=∠B=2∠C,则∠C=.8. 一个锐角三角形,所有内角的度数均为正整数,且最小角是最大角的 ,则这个锐角三角形三个内角的度数为 .
7. 在△ABC中,已知∠A=∠B=2∠C,则∠C=.8. 一个锐角三角形,所有内角的度数均为正整数,且最小角是最大角的 ,则这个锐角三角形三个内角的度数为 .三、解答题
-
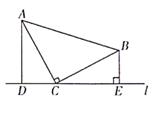
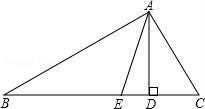
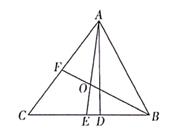
9. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数。
 10. 如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于F交AC于E,若∠A=48°,∠D=56°,求∠B和∠ACD的度数.
10. 如图,已知D为△ABC的边BC延长线上一点,DF⊥AB于F交AC于E,若∠A=48°,∠D=56°,求∠B和∠ACD的度数.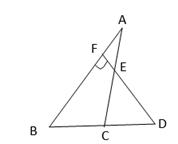
四、综合题