浙江省绍兴市柯桥区2020-2021学年七年级上学期数学期中联考试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、选择题(本大题共10小题，每小题2分，共20分)

1. －6的绝对值是（　　）

A、－6 B、6 C、 $\frac{1}{6}$ D、- $\frac{1}{6}$

查看试题解析
2. 绍兴市1月份某天最高气温是5℃，最低气温是－3℃，那么这天的温差(最高气温减最低气温)是（）

A、-2℃ B、8℃ C、-8℃ D、2℃

查看试题解析
3. 下列算式中，运算结果为负数的是（）

A、-（-2） B、 $| - 2 |$ C、 $（ - 2 ）^{3}$ D、 $（ - 2 ）^{2}$

查看试题解析
4. 下列各数中：－2，0.3， $\frac{22}{7}$ ， $\sqrt{2}$ ， $- π$ ， $- \sqrt{64}$ ，无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 下列各式中，计算正确的是（）

A、 $3 a^{2} - 2 a^{2} = 1$ B、 $3 a^{2} - 2 a^{2} = a$ C、 $3 a^{2} - 2 a = a^{2}$ D、 $3 a^{2} - 2 a^{2} = a^{2}$

查看试题解析
6. 已知 $- 25 a^{2 m} b$ 和 $7 b^{3 - n} a^{4}$ 是同类项，则 $m + n$ 的值是（）

A、2 B、3 C、4 D、6

查看试题解析
7. 下列说法正确的是（）

A、 $- m$ 一定表示负数 B、平方根等于它本身的数为0和1 C、倒数是本身的数为1 D、互为相反数的绝对值相等

查看试题解析
8. 如图，用10米长的铝合金做成一个长方形的窗框，设长方形窗框的横条长度为 x 米，则长方形窗框的面积为（）

A、 $x (10 - x)$ m² B、 $x (10 - 3 x)$ m² C、 $x (5 - \frac{3}{2} x)$ m² D、 $x (10 - \frac{3}{2} x)$ m²

查看试题解析
9. 如图所示的运算程序中，若开始输入的 $x$ 值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……第2019次输出的结果为（）

A、3 B、6 C、4 D、1

查看试题解析
10. 用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒。现在仓库里有若干张正方形和若干张长方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则库存中正方形纸板与长方形纸板之和的值可能是（）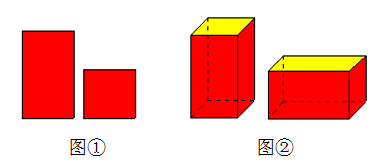

A、2018 B、2019 C、2020 D、2021

查看试题解析

二、填空题(本大题共10小题，每小题3分，共30分)

11. 5的倒数是， $- \frac{1}{8}$ 的立方根是， -2的相反数是

查看试题解析
12. 绝对值最小的数是；最大的负整数是；16的平方根是

查看试题解析
13. 单项式 $\frac{- {7x}^{3} y}{9}$ 的系数是，次数是

查看试题解析
14. 数轴上一个点到-2距离是5，那么这个点表示的数为．

查看试题解析
15. 对于两个不相等的实数a，b，定义一种新的运算： $a * b = \frac{\sqrt{a + b}}{a - b}$ ，例如： $3 * 2 = \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，那么15*（6*3）=.

查看试题解析
16. 若x，y为实数，且 $| x - 2 | + \sqrt{y + 3} = 0$ ，则 ${(x + y)}^{2019}$ 的值为

查看试题解析
17. 当m= ，多项式x²﹣mxy﹣3y²+ $\frac{1}{3}$ xy﹣1不含xy项．

查看试题解析
18. 已知代数式3x²－4x+6的值为-9，那么x²－ $\frac{4}{3}$ x+6的值为

查看试题解析
19. 观察下列图形的构成规律，根据此规律，第6个图形中有个圆，第n个图形中有个圆．

查看试题解析
20. 在1，3，5，……2017，2019，2021这1011数前面任意添加一个正号或负号，其代数和的绝对值最小值是

查看试题解析

三、解答题(本大题共8小题，共50分)

21. 计算：

(1)、 $8 + (- \frac{1}{4}) - 5 = (- 0.25)$

(2)、 $\sqrt[3]{- 8} + \sqrt{\frac{64}{81}} - | - 2 |$

(3)、 $(1 - \frac{1}{6} + \frac{3}{4}) \times (- 48)$

(4)、 $- 3^{2} \times {(- \frac{1}{3})}^{2} - {(- 2)}^{2} \div {(- \frac{1}{2})}^{2}$

查看试题解析
22. 在数轴上表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接： $\sqrt{4}$ ， $- (- 3)$ ， $- 3 \frac{1}{2}$ ，－1.5，

查看试题解析
23. 先化简再求值：
$- 3 （ x^{2} + y^{2} - x y ） + 2 (x^{2} - y^{2}) - 3 x y$ ，其中 $x = - 2$ ， $y = 1$ ．

查看试题解析

24. 据报道，某市受台风影响，10月6日的水位是2.83米，由于种种原因，水位一度超过警戒线。下表是该地区10月7日至12日的水位变化情况（单位：m）：

日期	7	8	9	10	11	12
水位记录	+1.41	+0.09	－0.04	+0.06	－0.45	－0.75

注：规定水位比前一天上升用“+”，比前一天下降用“－”，不升不降用“0”．

(1)、填空：该地区这6天内水位最高的一天是，实际水位是米；

(2)、与10月6日相比，10月12日该地区水位是上升了，还是下降了？变化了多少？

查看试题解析

25. 历史上的数学巨人欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ 来表示，即 $f (x) = x^{2} + 3 x - 5$ ，例如：当 $x = 1$ 时，多项式 $x^{2} + 3 x - 5$ 的值记为 $f (1) = 1^{2} + 3 \times 1 - 5$ =1。

(1)、已知 $f (x) = - 2 x^{2} - 3 x + 1$ ，分别求出 $f (- 1)$ 和 $f (- 2)$ 的值。

(2)、已知 $f (x) = a x^{3} + 2 x^{2} - x - 14$ ， $f (\frac{1}{2}) = a$ ，求 $a$ 的值。

查看试题解析
26. 某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：①西装和领带都按定价的90%付款；②买一套西装送一条领带．现某客户要到该服装厂购买x套西装（x≥1），领带条数比西装套数多5．

(1)、若该客户按方案①购买，需付款元：（用含x的代数式表示）若该客户按方案②购买，需付款元；（用含x的代数式表示）

(2)、若x=10，通过计算说明此时按哪种方案购买较为划算？

查看试题解析
27. 观察下列两个等式： $2 - \frac{1}{3} = 2 \times \frac{1}{3} + 1$ ， $5 - \frac{2}{3} = 5 \times \frac{2}{3} + 1$ ，给出定义如下：我们称使等式 $a - b = a b + 1$ 成立的一对有理数 $a$ ， $b$ 为“和谐数对”，
记为（ $a$ ， $b$ ），如：数对（ $2$ ， $\frac{1}{3}$ ），（ $5$ ， $\frac{2}{3}$ ）都是“和谐数对”．

(1)、数对（-3， $1$ ），（4， $\frac{3}{5}$ ）中是“和谐数对”的是；

(2)、若（ $x$ ， $y$ ）是“和谐数对”，则（ $- y$ ， $- x$ ）“和谐数对”（填“是”或“不是”）；

(3)、若（ $m$ ，5）是“和谐数对”，求 $m$ 的值；

查看试题解析
28. 如图，A、B分别为数轴上的两点，A点对应的数为﹣20，B点对应的数为100．

(1)、请写出与A、B两点距离相等的点M所对应的数；

(2)、现有一只电子蚂蚁P从B点出发，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C点相遇，你知道C点对应的数是多少吗?

(3)、若当电子蚂蚁P从B点出发时，以5个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3个单位/秒的速度也向左运动，请问：当它们运动多少时间时，两只蚂蚁间的距离为40个单位长度?

查看试题解析