浙江省绍兴市柯桥区2020-2021学年八年级上学期数学期中联考试卷
试卷更新日期：2020-12-17 类型：期中考试
一、选择题（本题有10小题，每小题2分，共20分）
-
1. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（ ）A、
B、
C、
D、
2. 做一个三角形的木架，以下四组木棒中，符合条件的是（ ）A、3cm，4cm，7cm B、4cm，5cm，6cm C、5cm，12cm，6cm D、1cm，2cm，3cm3. 已知a<b，则下列四个不等式中，不正确的是（ ）A、a+2<b+2 B、 C、 D、4. 下列命题的逆命题是真命题的是（ ）A、若 ，则 B、等边三角形是锐角三角形 C、相等的角是对顶角 D、全等三角形的面积相等5. 满足下列条件的△ABC，不是直角三角形的是（ ）A、a=5，b=12，c=13 B、 C、∠B=50°，∠C=40° D、∠A：∠B：∠C=3：4：56. 已知实数x，y满足 ，则以x，y的值为两边长的等腰三角形的周长是（ ）A、12或15 B、15 C、12 D、以上答案均不对7. 关于x的不等式3x﹣2a≤﹣2的解集如图所示，则a的值为（ ）
A、1 B、 C、﹣1 D、8. 在以下三个图形中，根据尺规作图的痕迹，不能判断射线AD平分∠BAC的是（ ）
A、图2 B、图1与图2 C、图1与图3 D、图2与图39. 如果三角形有一边上的中线长恰好等于这条边长，那么称这个三角形是“有趣三角形”，这条中线为“有趣中线”.如图，在△ABC中，∠C＝90°，较短的直角边BC＝ ，且△ABC是“有趣三角形”，则△ABC的“有趣中线”的长为（ ）
A、1 B、 C、2 D、10. 如图，在△ABC和△DBE中，AB=BC，DB=EB，∠ABC=∠DBE=50°.若∠BDC=25°，AD=4，DE= ，则CD的长为（ ）
A、 B、 C、 D、2二、填空题（本题有10小题，每小题3分，共30分）
-
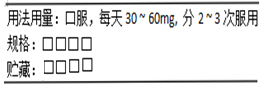
11. 等腰三角形的顶角是50°，则其底角的度数是.12. 可以用一个m的值说明命题“如果m能被2整除，那么它也能被4整除”是假命题，这个值可以是m＝ ．13. 已知直角三角形的两条直角边分别为5和12，则其斜边上的中线长为.14. 某种药品的说明书上贴有如图所示的标签，一次服用药品的剂量设为x，则x的取值范围是.
15. 如图，△ABC中，∠C=90°，AD平分∠BAC交BC于点D，BD：DC=2：1，BC=12cm，则D到AB的距离为cm.
16. 现定义一种新的运算：a*b=a2-2b.例如3*4=32-2×4=1，则不等式（-4）*x≥0的解集为.17. 如图，三角形纸片ABC中，AB=8cm，BC=6cm，AC=5cm.沿过点C的直线折叠，使点A落在BC边上的点E处，折痕为CD，则△BED的周长为cm.
18. 如图，△ABC为正三角形，BD是角平分线，点F在线段BD上移动，直线CF与AB交于点E，连结AF，当AE=AF时，∠BCE=°.
19. 如图，BP是∠ABC的平分线，AP⊥BP于P，连接PC，若△ABC的面积为1cm2 ， 则△PBC的面积为.
20. 如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B的路径运动，且速度为每秒1cm，设出发的时间为t秒.问t为时，△PBC构成等腰三角形？
三、解答题（本题有7小题，共50分，各小题都必须写出解答过程）
-
21.(1)、解不等式 ，并把解表达在数轴上.(2)、解不等式组22. 如图所示，在7×6的正方形网格中，选取14个格点，以其中三个格点为顶点画出△ABC，请你以选取的格点为顶点再画出一个三角形，且分别满足下列条件：
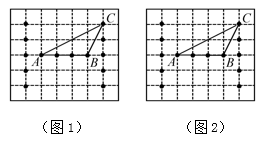(1)、图1中所画的三角形与△ABC组成的图形是轴对称图形；(2)、图2中所画的三角形与△ABC的面积相等，但不全等.23. 在Rt△ABC中，∠ACB＝90°，∠A＝40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)、求∠CBE的度数；(2)、过点D作DF//BE，交AC的延长线于点F，求∠F的度数.24. 如图， AB＝CD，AE⊥BC于E，DF⊥BC于F，AE＝DF.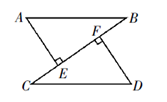
求证：
(1)、CE＝BF；(2)、AB//CD.25. 某家庭投资3.5万元资金建造屋顶光伏发电站，遇到晴天平均每天可发电30度，其他天气平均每天可发电5度，已知某月（按30天计）共发电600度.
(1)、求这个月晴天的天数；(2)、已知该家庭每月平均用电150度，若按每月发电600度计算，问至少需要几年才能收回成本？（不计其他费用，结果取整数）26. 如图，已知在△ABC中，∠BAC为直角，AB=AC，D为AC上一点，CE⊥BD于E，交BA的延长线于F.
(1)、求证：△ABD≌△ACF；(2)、若BD平分∠ABC，求证：CE= BD；(3)、若D为AC上一动点，∠AED如何变化？若变化，求它的变化范围；若不变，求出它的度数，并说明理由.27. 如图
(1)、问题发现与探究： 如图(1)，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=900 ， 点A、D、E在同一直线上，CM⊥AE于点M，连接BD，则①线段AE、BD之间的大小关系是 ， ∠ADB=°，并说明理由.
②求证：AD=2CM+BD.
(2)、问题拓展与应用：如图(2)，等腰Rt△ABC中，∠ACB=90°，过点A作直线，在直线上取点D，∠ADC=45°，连结BD，BD=1，AC= ，请在图(2)中画出图形并求出点C到该直线的距离.