浙江省湖州市吴兴区2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. -3的相反数是（）

A、3 B、-3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 《九章算术》中注有“今两算得失相反，要令正负以名之.”意思是：今有两数若其意义相反，则分别叫做正数与负数.若收入120元记作+120，则﹣40元表示（）

A、收入40元 B、收入80元 C、支出40元 D、支出80元

查看试题解析
3. 在0.010010001，0，π， $\sqrt{5}$ ， $\frac{22}{7}$ 中无理数的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
4. 2020年是不平凡的一年，新冠肺炎在武汉爆发，一方有难八方支援，很快各省市都斥巨资到抗疫前线，据有关部门初步统计，国家已经投入资金1390亿进行疫情防控，这个数据的背后不仅是抗击疫情的强力保障，更是祖国综合国力的直接体现，为此很多人高呼：此生无悔入华夏，来世再做中国人！请将1390亿用科学记数法表示为（　　）

A、 $1.39 \times 10^{4}$ B、 $1.39 \times 10^{11}$ C、 $1.39 \times 10^{12}$ D、 $1.39 \times 10^{10}$

查看试题解析
5. 绝对值不大于3.1的整数有（）个

A、4 B、5 C、6 D、7

查看试题解析
6. 下列各式中，正确的是（　　）

A、 $\sqrt{4} = \pm 2$ B、 $\pm \sqrt{9} = 3$ C、 $\pm \sqrt[3]{27} = \pm 3$ D、 $\sqrt{{(- 6)}^{2}} = - 6$

查看试题解析
7. 已知 $| x | = 6$ ， $y^{2} = 9$ ，且 $x y < 0$ ，则 $x + y$ 的值为（　　）

A、3或﹣3 B、9或3 C、15或3 D、9或﹣9

查看试题解析
8. 一辆汽车以80千米/时的速度行驶，从A城到B城需t小时，如果该车的速度增加v千米/时，那么从A城到B城需要（）

A、 $\frac{80 t}{v}$ B、 $\frac{80 t}{v + 80}$ C、 $\frac{v t}{v + 80}$ D、 $\frac{v t}{80}$

查看试题解析
9. 下列说法中错误的有（）个.
①若|x-4|＝x﹣4，则x＞4；②若a，b互为相反数，则 $\frac{a}{b} = - 1$ ；③平方等于本身的数是±1或0；④有理数与数轴上的点一一对应；⑤ $x^{2} - 2 x - x^{3} + 2^{5}$ 是五次四项式；⑥如果一个数有平方根，那么它一定有立方根

A、3个 B、4个 C、5个 D、6个

查看试题解析
10. 观察下列数 -1， 2，-3， 4，-5， 6，-7， 8 ......将这列数排成下列形式：
$\begin{array}{l} \begin{matrix} \end{matrix} - 1 \\ \begin{matrix} \end{matrix} 2 \begin{matrix} \end{matrix} - 3 \begin{matrix} \end{matrix} 4 \\ \begin{matrix} - 5 & 6 \end{matrix} \begin{matrix} \end{matrix} - 7 \begin{matrix} \end{matrix} 8 \begin{matrix} \end{matrix} - 9 \\ 10 \begin{matrix} \end{matrix} - 11 \begin{matrix} \end{matrix} 12 \begin{matrix} \end{matrix} - 13 \begin{matrix} \end{matrix} 14 \begin{matrix} \end{matrix} - 15 \begin{matrix} \end{matrix} 16 \\ \begin{matrix} \end{matrix} ............ \end{array}$

按照上述规律排下去，那么第30行从左边数第5个数是（）

A、846 B、-846 C、847 D、-847

查看试题解析

二、填空题（每小题4分，共24分）

11. $\sqrt{{(- 2)}^{2}}$ 的平方根是； $8 a^{3}$ 的立方根是 .

查看试题解析
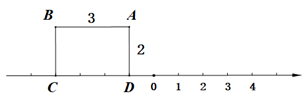
12. 单项式 $π a$ 的次数是；整式 $- \frac{3 x^{3} + 2 x^{2} + 1}{7}$ 的二次项系数为.

查看试题解析
13. 用科学记数法表示88000000为； $2.1 \times 10^{5}$ 精确到位.

查看试题解析
14. 定义新运算： $a * b = \frac{{(a - b)}^{2}}{a + b}$ ，则2*4= .

查看试题解析
15. 若 $a b c \neq 0$ ，则 $\frac{| a b |}{a b} + \frac{| b c |}{b c} + \frac{| a c |}{a c}$ = .

查看试题解析
16. 一个长方形ABCD在数轴上的位置如图所示，AB=3，AD=2，若此长方形绕着顶点按照顺时针方向在数轴上连续翻转，翻转1次后，点A所对应的数为1，求翻转2018次后，点B所对应的数.

查看试题解析

三、简答题（17、18、 19题各6分，20、21题各8分，22、23题各10分，24题12分共66分）

17. 计算

(1)、- $12 \times （ \frac{1}{3} - \frac{1}{4} + 1 ） \times 2 + （ - 1 ）^{2019}$

(2)、 $- 1^{2} + \sqrt[3]{8} \div （ 3 - 5 ） + | \sqrt{5} - 3 |$

查看试题解析
18. 已知 $x - 2$ 与 $- 4 x + 14$ 是y的平方根.求y与-2的立方的差.

查看试题解析
19. 把 $- （ - 2 ）， \begin{matrix} \end{matrix} \sqrt[3]{3 \frac{3}{8}} ， \begin{matrix} \end{matrix} - \sqrt{9} ， \begin{matrix} \end{matrix} | - 5 |$ 四个数表示在数轴上，并用“＞”号连接起来.

查看试题解析
20. 如图所示，有长为 $l$ 的篱笆，利用它和一面墙围城长方形园子，在园子的长边上开了1米的门，园子的宽为 $t$ .

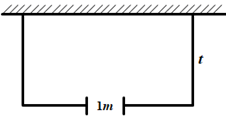(1)、用关于l，t的代数式表示园子的面积.

(2)、当l=100m，t=30m时，求园子的面积.

查看试题解析
21. 如图，在甲乙两个4×4的方格图中，每个小正方形的边长都为1.

(1)、请求出图中阴影正方形的边长；

(2)、大家知道 $\sqrt{2}$ 是无理数， $且 1 < \sqrt{2} < 2$ ，∴它的整数部分为1，小数部分可以表示为 $\sqrt{2} - 1$ .请在图乙中画一个与图甲阴影部分面积不相等的正方形，要求边长为无理数，并求所画正方形边长的整数部分.

(3)、 $5 + \sqrt{3}$ 的整数部分是；小数部分是 .

查看试题解析
22. 股民小罗上星期五记录某公司股票收盘价为每股20元，下表为本周内每日该股票的涨跌情况.（单位：元）（注：股市星期一至星期五开市，星期六、星期日休息）

星期

一

二

三

四

五

每股涨跌

+4

﹣2

+4.5

﹣2.5

﹣3

(1)、星期四收盘时，每股是多少元？

(2)、本周每股最高元，最低元.

(3)、已知小罗买进股票时付了总交易额1.5‰的手续费，卖出时还要付成交额1.5‰（1.5‰读作千分之1.5）的手续费和1‰的交易税，如果小罗以上周五的收盘价买入1000股，并以本周五收盘价全部卖出股票，他赚了或赔了多少钱？（温馨提示：股市有风险，入市需谨慎）

查看试题解析
23. 探究：
$\begin{array}{l} 2^{2} - 2^{1} = 2 \times 2^{1} - 1 \times 2^{1} = 2^{（ \begin{matrix} \end{matrix} ）} \\ 2^{3} - 2^{2} = \underline{\begin{matrix} \end{matrix}} = 2^{（ \begin{matrix} \end{matrix} ）} \\ 2^{4} - 2^{3} = \underline{\begin{matrix} \end{matrix}} = 2^{（ \begin{matrix} \end{matrix} ）} \end{array}$

……

(1)、请仔细观察，写出第5个等式；

(2)、请你找规律，写出第n个等式；

(3)、计算： $2^{} + 2^{2} + \cdot \cdot \cdot + 2^{2018} + 2^{2019} - 2^{2020}$ .

查看试题解析
24. 对于数轴上的A，B，C三点，给出如下定义：若其中一个点与其他两个点的距离恰好满足2倍的数量关系，则称该点是其他两点的“友好点”.例如数轴上点A，B，C所表示的数分别为1，3，4，满足AB＝2BC，此时点B是点A，C的“友好点”.现在，数轴上有M，N两点，它们表示的数为-2，4 .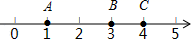

(1)、数轴上点 $D_{1} ， D_{2} ， D_{3}$ 分別对应-4，0，5，这三个点中，点是点M，N的“友好点”；点N是两点的“友好点”；

(2)、动点P，Q分别从M，N两点出发，以2cm/s，1cm/s的速度同时向右运动，且满足M、P、Q三点中其中一个点是另外两点的“友好点”.求点P的运动时间t.

查看试题解析

星期	一	二	三	四	五
每股涨跌	+4	﹣2	+4.5	﹣2.5	﹣3