浙江省湖州市吴兴区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-17 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. ⊙O的半径为8cm,点A到圆心O的距离为6cm,则点A与⊙O的位置关系是( )A、点A在圆内 B、点A在圆上 C、点A在圆外 D、不能确定2. 把抛物线 向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、3. 下列事件中,必然事件是( )A、2月份有31天 B、一个等腰三角形中,有两条边相等 C、明天的太阳从西边出来 D、投掷一枚质地均匀的骰子,出现6点向上4. 如图,四边形ABCD为圆内接四边形∠A=85°,∠B=105°,则∠C的度数为( )
 A、115° B、75° C、95° D、不能确定5. 下列函数中,y总随x的增大而减小的是( )A、y=4x B、y=﹣4x C、y=x﹣4 D、y=x26. 如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( )
A、115° B、75° C、95° D、不能确定5. 下列函数中,y总随x的增大而减小的是( )A、y=4x B、y=﹣4x C、y=x﹣4 D、y=x26. 如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,﹣1),则△ABC外接圆的半径为( ) A、2 B、3 C、4 D、7. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
A、2 B、3 C、4 D、7. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( ) A、 B、 C、 D、8. 如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A、 B、 C、 D、8. 如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( ) A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF=FD9. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心( ).
A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF=FD9. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心( ). A、 B、 C、 D、10. 如图,平面直角坐标系中,已知 , ,P为y轴正半轴上一个动点,将线段 绕点P逆时针旋转 ,点A的对应点为Q,则线段 的最小值是( )
A、 B、 C、 D、10. 如图,平面直角坐标系中,已知 , ,P为y轴正半轴上一个动点,将线段 绕点P逆时针旋转 ,点A的对应点为Q,则线段 的最小值是( )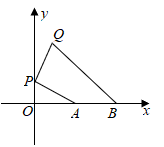 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:(本题有6小题,每小题4分,共24分)
-
11. 抛物线 的对称轴是.12. 如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为.
 13. 如图,在Rt△ACB中,∠ACB=90°,∠A=27°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数是.
13. 如图,在Rt△ACB中,∠ACB=90°,∠A=27°,将△ABC绕点C逆时针旋转α角到△A1B1C的位置,A1B1恰好经过点B,则旋转角α的度数是. 14. 现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x,小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为.15. 如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
14. 现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x,小明掷B立方体朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为.15. 如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①若点M(﹣2,y1)、点N( ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
②将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;
③抛物线y=﹣x2+2x+m+1与直线y=m+3有且只有一个交点;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 .
其中正确判断的序号是.
 16. 如图,矩形纸片ABCD中,BC=5,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC′D;作∠BPC′的角平分线,交AB于点E.设BP=x,BE=y,则y与x的函数关系式为.
16. 如图,矩形纸片ABCD中,BC=5,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC′D;作∠BPC′的角平分线,交AB于点E.设BP=x,BE=y,则y与x的函数关系式为.
三、解答题:(本题有8个小题,共66分)
-
17. 已知等腰三角形ABC,如图.
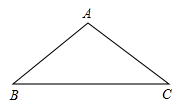 (1)、用直尺和圆规作△ABC的外接圆;(2)、设△ABC的外接圆的圆心为O,若∠BOC=128°,求∠BAC的度数.18. 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)、用直尺和圆规作△ABC的外接圆;(2)、设△ABC的外接圆的圆心为O,若∠BOC=128°,求∠BAC的度数.18. 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m. (1)、在如图的坐标系中求抛物线的解析式;(2)、若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?19. 在湖州创建国家卫生文明城市的过程中,小辉和小明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
(1)、在如图的坐标系中求抛物线的解析式;(2)、若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?19. 在湖州创建国家卫生文明城市的过程中,小辉和小明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:①清理类岗位:清理花坛卫生死角;清理楼道杂物(分别用 表示)。
②宣传类岗位:垃圾分类知识宣传;交通安全知识宣传(分别用 表示)。
(1)、小辉同学从四个岗位中随机选取一个报名,恰好选择清理类岗位概率为是;(2)、若小辉和小明各随机从四个岗位中选一个报名,请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率.20. 如图,二次函数y=﹣x2+4x+m的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点D,点A的坐标是(﹣1,0),C是抛物线的顶点. (1)、求二次函数的解析式;(2)、当0<x<5时,求y的取值范围;(3)、连接BC,线段OD上有一点E,点E关于抛物线的对称轴的对称点F恰好在线段BC上,求点E的坐标.21. 如图,圆内接四边形ABCD,AB是⊙O的直径,OD∥AC交BC于点E.
(1)、求二次函数的解析式;(2)、当0<x<5时,求y的取值范围;(3)、连接BC,线段OD上有一点E,点E关于抛物线的对称轴的对称点F恰好在线段BC上,求点E的坐标.21. 如图,圆内接四边形ABCD,AB是⊙O的直径,OD∥AC交BC于点E. (1)、求证:△BCD为等腰三角形;(2)、若BE=4,AC=6,求DE.22. 某宾馆有 50 个房间供游客居住,当每个房间的定价为每天 160 元时,房间会全部住满,当每个房间每天的定价每增加 10 元时,就会有一个房间空闲,如果游客居住房间, 宾馆需对每个房间每天支出 20 元的各种费用.设每个房间的定价为 x 元时,相应的住房数为 y 间.(1)、求 y 与 x 的函数关系式;(2)、定价为多少时宾馆当天利润 w 最大?并求出一天的最大利润;(3)、若老板决定每住进去一间房就捐出 a 元(a≤30)给当地福利院,同时要保证房间定价 x 在 160 元至 350 元之间波动时(包括两端点),利润 w 随 x 的增大而增大,求 a 的取值范围23. 定义:如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征轴三角形”.显然,“特征轴三角形”是等腰三角形.(1)、抛物线y=x2﹣2 x对应的“特征轴三角形”是;抛物线y= x2﹣2对应的“特征轴三角形”是.(把下列较恰当结论的序号填在横线上:①腰与底边不相等的等腰三角形;②等边三角形;③非等腰的直角三角形;④等腰直角三角形.)(2)、若抛物线y=ax2+2ax﹣3a对应的“特征轴三角形”是直角三角形,请求出a的值.(3)、如图,面积为12 的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“特征轴三角形”,求此抛物线的解析式.
(1)、求证:△BCD为等腰三角形;(2)、若BE=4,AC=6,求DE.22. 某宾馆有 50 个房间供游客居住,当每个房间的定价为每天 160 元时,房间会全部住满,当每个房间每天的定价每增加 10 元时,就会有一个房间空闲,如果游客居住房间, 宾馆需对每个房间每天支出 20 元的各种费用.设每个房间的定价为 x 元时,相应的住房数为 y 间.(1)、求 y 与 x 的函数关系式;(2)、定价为多少时宾馆当天利润 w 最大?并求出一天的最大利润;(3)、若老板决定每住进去一间房就捐出 a 元(a≤30)给当地福利院,同时要保证房间定价 x 在 160 元至 350 元之间波动时(包括两端点),利润 w 随 x 的增大而增大,求 a 的取值范围23. 定义:如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“特征轴三角形”.显然,“特征轴三角形”是等腰三角形.(1)、抛物线y=x2﹣2 x对应的“特征轴三角形”是;抛物线y= x2﹣2对应的“特征轴三角形”是.(把下列较恰当结论的序号填在横线上:①腰与底边不相等的等腰三角形;②等边三角形;③非等腰的直角三角形;④等腰直角三角形.)(2)、若抛物线y=ax2+2ax﹣3a对应的“特征轴三角形”是直角三角形,请求出a的值.(3)、如图,面积为12 的矩形ABCO的对角线OB在x轴的正半轴上,AC与OB相交于点E,若△ABE是抛物线y=ax2+bx+c的“特征轴三角形”,求此抛物线的解析式. 24. 如图,已知抛物线y=ax2+bx+5经过A(﹣5,0),B(﹣4,﹣3)两点,与x轴的另一个交点为C,顶点为D,连接BD,CD.
24. 如图,已知抛物线y=ax2+bx+5经过A(﹣5,0),B(﹣4,﹣3)两点,与x轴的另一个交点为C,顶点为D,连接BD,CD. (1)、求该抛物线的表达式;(2)、点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
(1)、求该抛物线的表达式;(2)、点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.①当点P在直线BC的下方运动时,求△PBC的面积的最大值
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.