初中数学北师大版八年级上学期期末考试复习专题:07 二元一次方程与一次函数
试卷更新日期:2020-12-17 类型:复习试卷
一、单选题
-
1. 如图,是在同一坐标系内作出的一条函数的图象l1 , l2 , 设y=k1x+b1 , y=k2x+b2 , 则方程组 的解是( ).
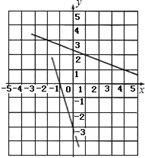 A、 B、 C、 D、不能确定2. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、3. 如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
A、 B、 C、 D、不能确定2. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、3. 如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( ) A、(2,8) B、 C、 D、(4,12)4. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ x﹣1的图像的交点坐标为( )A、(﹣4,1) B、(1,﹣4) C、(4,﹣1) D、(﹣1,4)
A、(2,8) B、 C、 D、(4,12)4. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ x﹣1的图像的交点坐标为( )A、(﹣4,1) B、(1,﹣4) C、(4,﹣1) D、(﹣1,4)二、填空题
-
5. 如图,函数y=ax+b和y=kx的图象交于一点,则二元一次方程组 的解是 .
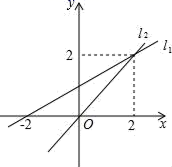 6. 如图,在平面直角坐标系中,直线 和 相交于点(2,-1),则关于 、 的方程组 的解为 .
6. 如图,在平面直角坐标系中,直线 和 相交于点(2,-1),则关于 、 的方程组 的解为 .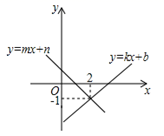 7. 如图,直线 和直线 相交于点M,若关于 的方程组 的解是 ,那么 = .
7. 如图,直线 和直线 相交于点M,若关于 的方程组 的解是 ,那么 = .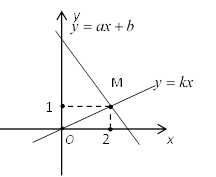
三、综合题
-
8. 已知一次函数y=(n
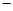 4)x+(4
4)x+(4 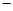 2m )和y=(n+1)x+m
2m )和y=(n+1)x+m 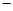 3.
(1)、若它们的图象与y轴的交点分别是点P和点Q.若点P与点Q关于x轴对称,m的值为;(2)、若这两个一次函数的图象交于点(1,2),则m,n的值为 .9. 为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
3.
(1)、若它们的图象与y轴的交点分别是点P和点Q.若点P与点Q关于x轴对称,m的值为;(2)、若这两个一次函数的图象交于点(1,2),则m,n的值为 .9. 为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
A B 甲 20 25 乙 15 24 (1)、求甲乙两厂各生产了这批防疫多少吨?(2)、设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,并设计使总运费最少的调运方案;(3)、当每吨运费降低m元,( 且m为整数),按(2)中设计的调运方案运输,总运费不超过5200元,求m的最小值.10. 某经销商从市场得知如下信息:A品牌手机
B品牌手机
进价(元/部)
700
100
售价(元/部)
900
160
他计划用4万元资金一次性购进这两种品牌手机共100部,设该经销商购进A品牌手机X部,这两种品牌手机全部销售完后获得利润为y元。
(1)、试写出y与x之间的函数关系式:
(2)、若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)、选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
11. 下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。电瓶车
公交车
货车
小轿车
合计(车流总量)
(第一时段)8:50~9:00
m
86
161
(第二时段)9:00~9:10
7n
m
n
99
合计
30
185
(1)、根据表格信息,在表格中填写第一时段电瓶车和货车的数量。(2)、在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为170辆。①求m,n的值。
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加1辆公交车,可减少8辆小轿车和5辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?