浙江省杭州市萧山区六校2021届九年级上学期数学期中联考试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、选择题（本题有10个小题，每小题3分，共30分）

1. 二次函数y=x²﹣2x﹣3图象与y轴的交点坐标是（）

A、（0，1） B、（1，0） C、（-3，0） D、（0，-3）

查看试题解析
2. 将抛物线y＝2x²经过怎样的平移可得到抛物线y＝2(x＋3)²＋4 （）

A、先向左平移3个单位长度，再向上平移4个单位长度 B、先向左平移3个单位长度，再向下平移4个单位长度 C、先向右平移3个单位长度，再向上平移4个单位长度 D、先向右平移3个单位长度，再向下平移4个单位长度

查看试题解析
3. 用配方法将二次函数y＝x²－8x－9化为y＝a(x-h)²＋k的形式为( )

A、y＝(x－4)²＋7 B、y＝(x－4)²－25 C、y＝(x＋4)²＋7 D、y＝(x＋4)²－25

查看试题解析
4. 一个布袋里装有3个只有颜色不同的球，其中2个红球，1个白球，从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，则两次摸到的球都是白球的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{9}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
5. 已知抛物线y＝ax²﹣2ax（a>0）的图象上三个点的坐标分别为A（﹣1，y₁），B（2，y₂），C（4，y₃），则y₁ ， y₂ ， y₃的大小关系为（）

A、y₃＞y₁＞y₂ B、y₃＞y₂＞y₁ C、y₂＞y₁＞y₃ D、y₂＞y₃＞y₁

查看试题解析
6. 在Rt△ABC中，∠C=90°，AC=6，BC=8，D是AB边上的中点以点C为圆心，6为半径作圆，则点D与⊙C的位置关系是（）

A、点D在⊙C内 B、点D在⊙C上 C、点D在⊙C外 D、不能确定

查看试题解析
7. 如图，BC是⊙O的直径，A ， D是⊙O上的两点，连接AB ， AD ， BD ，若∠ADB＝70°，则∠ABC的度数是（）

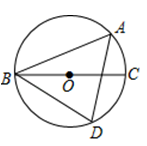A、20° B、70° C、30° D、90°

查看试题解析
8. 如图，在⊙O中，弦 $A B ⊥ B C$ ，AB=6，BC=8，D是 $\overset{⌢}{BC}$ 上一点，弦AD与BC所夹锐角度数是72°，则 $\overset{⌢}{BD}$ 的长为( )

A、 $\frac{1}{2} π$ B、 $π$ C、 $2 π$ D、 $5 π$

查看试题解析
9. 如图，在半径为 $\sqrt{13}$ 的⊙O中，弦AB与CD交于点E，∠DEB＝75°，AB＝6，AE＝1，则CD的长是（）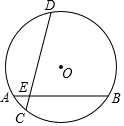

A、2 $\sqrt{6}$ B、2 $\sqrt{10}$ C、2 $\sqrt{11}$ D、4 $\sqrt{3}$

查看试题解析
10. 已知二次函数y₁=mx²+4mx﹣5m（m≠0），一次函数y₂=2x﹣2，有下列结论：
①当x＞﹣2时，y₁随x的增大而减小；②二次函数y₁=mx²+4mx﹣5m（m≠0）的图象与x轴交点的坐标为（﹣5，0）和（1，0）；③当m=1时，y₁≤y₂；④在实数范围内，对于x的同一个值，这两个函数所对应的函数值y₂≤y₁均成立，则 $m = \frac{1}{3}$ ．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（本题有6个小题，每小题4分，共24分）

11. 如图，一块飞镖游戏板由大小相等的小正方形构成，向游戏板随机投掷一枚飞镖（飞镖每次都落在游戏板上），击中黑色区域的概率是.

查看试题解析
12. 如图，若抛物线y＝ax²＋bx＋c上的P(4，0)， Q两点关于它的对称轴x＝1对称，则点Q的坐标为．

查看试题解析
13. 如图，已知正五边形ABCDE内接于⊙O ，连结BD ，则∠ABD的度数是

查看试题解析
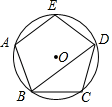14. 若函数y＝x²+x＋c的图像与坐标轴有三个交点，则c的取值范围是．

查看试题解析
15. 已知二次函数y=ax²-6ax-2（a为常数）的图象不经过第二象限，在自变量x的值满足1≤x≤2时，其对应的函数值y的最大值为3，则a的值为

查看试题解析
16. 如图，在 $Δ A B C$ 中， $A C = B C = 5$ ， $A B = 6$ ，点D为AC上一点，作 $D E / / A B$ 交BC于点E ，点C关于DE的对称点为点O ，以OA为半径作⊙O恰好经过点C ，并交直线DE于点M ， N则MN的值为．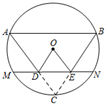

查看试题解析

三、解答题（本题有7个小题，共66分）

17. 已知二次函数y=﹣2x²+4x+6．

(1)、求出该函数的顶点坐标，图象与x轴的交点坐标，

(2)、当x在什么范围内时，y随x的增大而增大？当x在什么范围内时，y随x的增大而减小？当x在什么范围内时，y＞0？

查看试题解析
18. 甲、乙两个袋中均有三张除所标数字外其余完全相同的卡片（如图所示）.现先从甲袋中随机取出一张卡片，用x表示取出的卡片上的数，再从乙袋中随机取出一张卡片，用y表示取出的卡片上的数，把x，y分别作为点A的横坐标和纵坐标.

(1)、请用列表或画树状图的方法表示出点A的坐标（x，y）的所有情况；

(2)、求点A落在第一象限内的概率．

查看试题解析
19. 如图，在⊙O中， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ，CD⊥OA于D ， CE⊥OB于E.求证：AD＝BE.

查看试题解析
20. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为
A（﹣3，5），B（﹣2，1），C（﹣1，3）

（ 1 ）若△ABC经过平移后得到的△A₁B₁C₁ ，已知点C₁的坐标为（4，0），写出顶点A₁ ， B₁的坐标；

（ 2 ）若△ABC和△A₂B₂C₂关于原点O成中心对称图形，写出△A₂B₂C₂的各顶点的坐标；

（ 3 ）将△ABC绕着点O按顺时针方向旋转90°得到△A₃B₃C₃ ，画出△A₃B₃C₃并写出△A₃B₃C₃的各顶点的坐标．

查看试题解析
21. 如图，点C ， D是半圆O上的三等分点，直径AB＝4，连接AD ， AC ，作DE⊥AB ，垂足为E ， DE交AC于点F ．

(1)、求证：AF＝DF ．

(2)、求阴影部分的面积

查看试题解析
22. 已知一次函数y₁＝2x+b的图象与二次函数y₂＝a（x²+bx+1）（a≠0，a、b为常数）的图象交于A、B两点，且A的坐标为（0，1）.

(1)、求出a、b的值，并写出y₁ ， y₂的表达式；

(2)、验证点B的坐标为（1，3），并写出当y₁≥y₂时，x的取值范围；

(3)、设u＝y₁+y₂ ， v＝y₁﹣y₂ ，若m≤x≤n时，u随着x的增大而增大，且v也随着x的增大而增大，求m的最小值和n的最大值.

查看试题解析
23. 已知P是⊙O上一点，过点P作不过圆心的弦PQ，在劣弧PQ和优弧PQ上分别有动点A、B（不与P，Q重合），连接AP、BP．若∠APQ＝∠BPQ．

(1)、如图1，当∠APQ＝45°，AP＝1，BP＝ $2 \sqrt{2}$ 时，求⊙O的半径；

(2)、在（1）的条件下，求四边形APBQ的面积

(3)、如图2，连接AB，交PQ于点M，点N在线段PM上（不与P、M重合），连接ON、OP，若∠NOP+2∠OPN＝90°，探究直线AB与ON的位置关系，并说明理由．

查看试题解析