广西柳州市2020年中考数学试卷
试卷更新日期:2020-12-17 类型:中考真卷
一、单选题
-
1. ﹣ 的绝对值是( )A、5 B、﹣5 C、﹣ D、2. 如图,这是一个由5个完全相同的小正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、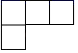 C、
C、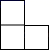 D、
D、 3. 下列四个图案中,是中心对称图形的是( )A、
3. 下列四个图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 2020年是我国全面建成小康社会收官之年,我市将全面完成剩余19700贫困人口脱贫的任务.用科学记数法将数据19700表示为( )A、 0.197×105 B、1.97×104 C、19.7×103 D、197×1025. 为了解学生体育锻炼的用时情况,陈老师对本班50名学生一天的锻炼时间进行调查,并将结果绘制成如图统计图,那么一天锻炼时间为1小时的人数占全班人数的( )
4. 2020年是我国全面建成小康社会收官之年,我市将全面完成剩余19700贫困人口脱贫的任务.用科学记数法将数据19700表示为( )A、 0.197×105 B、1.97×104 C、19.7×103 D、197×1025. 为了解学生体育锻炼的用时情况,陈老师对本班50名学生一天的锻炼时间进行调查,并将结果绘制成如图统计图,那么一天锻炼时间为1小时的人数占全班人数的( ) A、14% B、16% C、20% D、50%6. 如图,点A、B、C在⊙O上,若∠BOC=70°,则∠A的度数为( )
A、14% B、16% C、20% D、50%6. 如图,点A、B、C在⊙O上,若∠BOC=70°,则∠A的度数为( ) A、35° B、40° C、55° D、70°7. 通过如下尺规作图,能确定点D是BC边中点的是( )A、
A、35° B、40° C、55° D、70°7. 通过如下尺规作图,能确定点D是BC边中点的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB= =( )
8. 如图,在Rt△ABC中,∠C=90°,AB=4,AC=3,则cosB= =( )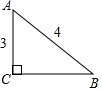 A、 B、 C、 D、9. 2ab•a2的计算结果是( )A、 2ab B、4ab C、2a3b D、4a3b10. 如图是甲、乙两名射击运动员10次射击成绩的折线统计图,根据折线图判断下列说法正确的是( )
A、 B、 C、 D、9. 2ab•a2的计算结果是( )A、 2ab B、4ab C、2a3b D、4a3b10. 如图是甲、乙两名射击运动员10次射击成绩的折线统计图,根据折线图判断下列说法正确的是( )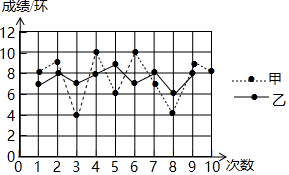 A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、无法判断谁的成绩更稳定11. 下列多项式中,能用平方差公式进行因式分解的是( )A、a2﹣b2 B、﹣a2﹣b2 C、a2+b2 D、a2+2ab+b212. 甲、乙二人做某种零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,若设乙每小时做 个,则可列方程( )A、 B、 C、 D、
A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、无法判断谁的成绩更稳定11. 下列多项式中,能用平方差公式进行因式分解的是( )A、a2﹣b2 B、﹣a2﹣b2 C、a2+b2 D、a2+2ab+b212. 甲、乙二人做某种零件,已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,若设乙每小时做 个,则可列方程( )A、 B、 C、 D、二、填空题
-
13. 如图,直线l2 , l3被直线l1所截,l2 l3 , 已知∠1=80°,则∠2=.
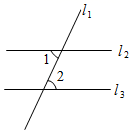 14. 一元一次方程2x﹣8=0的解是x=.15. 若分式 有意义,则 的取值范围是.16. 点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为.17. 如图,每一幅图中有若干个菱形,第1幅图中有1个菱形,第2幅图中有3菱形.第3幅图中有5个菱形,依照此规律,第6幅图中有个菱形.
14. 一元一次方程2x﹣8=0的解是x=.15. 若分式 有意义,则 的取值范围是.16. 点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为.17. 如图,每一幅图中有若干个菱形,第1幅图中有1个菱形,第2幅图中有3菱形.第3幅图中有5个菱形,依照此规律,第6幅图中有个菱形.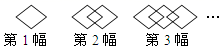 18. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的H处,有下列结论:①∠EBG=45°;②2S△BFG=5S△FGH;③△DEF∽△ABG;④4CE=5ED.其中正确的是.(填写所有正确结论的序号)
18. 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的H处,有下列结论:①∠EBG=45°;②2S△BFG=5S△FGH;③△DEF∽△ABG;④4CE=5ED.其中正确的是.(填写所有正确结论的序号)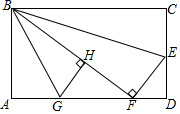
三、解答题
-
19. 计算: .20. 如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
 21. 解不等式组 请结合解题过程,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在如图所示的数轴上表示出来:
21. 解不等式组 请结合解题过程,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在如图所示的数轴上表示出来: (4)、原不等式的解集为.22. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
(4)、原不等式的解集为.22. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)23. 如图,已知▱ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)23. 如图,已知▱ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.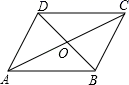 (1)、求△ADO的周长;(2)、求证:△ADO是直角三角形.24. 如图,平行于y轴的直尺(部分)与反比例函数 (x>0)的图象交于A、C两点,与x轴交于B、D两点,连接AC,点A、B对应直尺上的刻度分别为5、2,直尺的宽度BD=2,OB=2.设直线AC的解析式为y=kx+b.
(1)、求△ADO的周长;(2)、求证:△ADO是直角三角形.24. 如图,平行于y轴的直尺(部分)与反比例函数 (x>0)的图象交于A、C两点,与x轴交于B、D两点,连接AC,点A、B对应直尺上的刻度分别为5、2,直尺的宽度BD=2,OB=2.设直线AC的解析式为y=kx+b.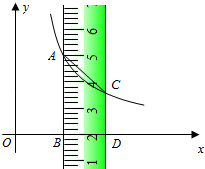 (1)、请结合图象,直接写出:
(1)、请结合图象,直接写出:①点A的坐标是;
②不等式 的解集是;
(2)、求直线AC的解析式.25. 如图,AB为⊙O的直径,C为⊙O上的一点,连接AC、BC,OD⊥BC于点E,交⊙O于点D,连接CD、AD,AD与BC交于点F,CG与BA的延长线交于点G.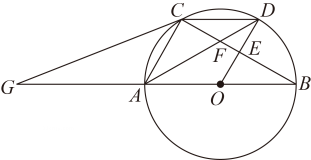 (1)、求证:△ACD∽△CFD;(2)、若∠CDA=∠GCA,求证:CG为⊙O的切线;(3)、若sin∠CAD= ,求tan∠CDA的值.26. 如图①,在平面直角坐标系xOy中,批物线y=x2﹣4x+a(a<0)与y轴交于点A,与x轴交于E、F两点(点E在点F的右侧),顶点为M.直线 与x轴、y轴分别交于B、C两点,与直线AM交于点D.
(1)、求证:△ACD∽△CFD;(2)、若∠CDA=∠GCA,求证:CG为⊙O的切线;(3)、若sin∠CAD= ,求tan∠CDA的值.26. 如图①,在平面直角坐标系xOy中,批物线y=x2﹣4x+a(a<0)与y轴交于点A,与x轴交于E、F两点(点E在点F的右侧),顶点为M.直线 与x轴、y轴分别交于B、C两点,与直线AM交于点D.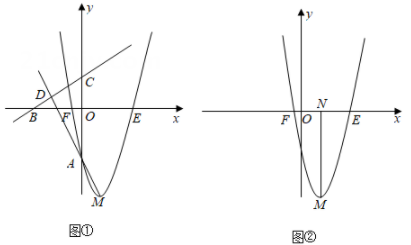 (1)、求抛物线的对称轴;(2)、在y轴右侧的抛物线上存在点P,使得以P、A、C、D为顶点的四边形是平行四边形,求a的值;(3)、如图②,过抛物线顶点M作MN⊥x轴于N,连接ME,点Q为抛物线上任意一点,过点Q作QG⊥x轴于G,连接QE.当a=﹣5时,是否存在点Q,使得以Q、E、G为顶点的三角形与△MNE相似(不含全等)?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的对称轴;(2)、在y轴右侧的抛物线上存在点P,使得以P、A、C、D为顶点的四边形是平行四边形,求a的值;(3)、如图②,过抛物线顶点M作MN⊥x轴于N,连接ME,点Q为抛物线上任意一点,过点Q作QG⊥x轴于G,连接QE.当a=﹣5时,是否存在点Q,使得以Q、E、G为顶点的三角形与△MNE相似(不含全等)?若存在,求出点Q的坐标;若不存在,请说明理由.