浙江省温岭市团队六校2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2020-12-17 类型：期中考试
一、单选题
-
1. 在下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列线段能组成三角形是（ ）A、1、2、3 B、4、5、6 C、6、8、14 D、5、6、133. 如图，已知∠ABC＝∠BAD ， 添加下列条件还不能判定△ABC≌△BAD的是（ ）
A、AC＝BD B、∠CAB＝∠DBA C、∠C＝∠D D、BC＝AD4. 已知点M（3，－1）关于y轴对称的的对称点N的坐标为（a＋b，1－b），则ab的值为（ ）A、10 B、25 C、－3 D、325. 在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是（ ）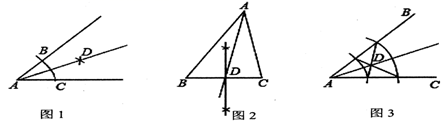
A、图1与图2 B、图1与图3 C、图2与图3 D、图1、图2、图36. 如图，在△ABC中，∠A=105º，AC的垂直平分线MN交BC于点E，AB＋BE=BC，则∠B的度数是（ ）
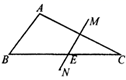A、45º B、50º C、55º D、60º7. 如图，是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击出，该球最后落入1号袋，经过反射的次数是（ ）
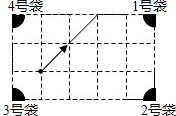A、4次 B、5次 C、6次 D、7次8. 已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）A、6条 B、7条 C、8条 D、9条9. 等边三角形ABC的边长为1，点P在AB上，PQ⊥BC，QR⊥AC，RS⊥AB，其中Q，R，S为垂足，若SP＝ ，则AP的长是（ ）
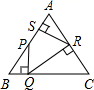A、 B、 C、 D、 或10. 如图，∠BAC=90º，AB=AC=6，BE=2，DE=3，∠BDE=15º，点P在线段AE上，PD=DE，△ADQ是等边三角形，连接PQ交AC于点F，则PF的长为（ ）
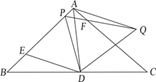A、2 B、3 C、 D、二、填空题
-
11. 在△ABC中，∠A＝40°，∠B＝60°，则∠C＝°．12. 如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12，则图中△BEF的面积为。
13. 在如图所示的方格中，连接格点AB、AC，则∠1+∠2＝度.
14. 如图，AB∥CD，AD与BC交于点O，OP平分∠BOD，交CO的延长线于P，若∠A=100º，∠B=30º，则∠P的度数是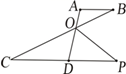
15. 我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”．如果等腰三角形的“内角正度值”为45°，那么该等腰三角形的顶角等于 ．16. 如图，四边形ABCD中，AB = BC，∠ABC =∠CDA = 90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE =；
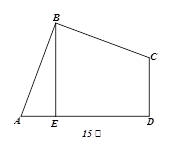17. 如图，在△AOB中，∠OAB=∠AOB=15º，OB=5，OC平分∠AOB，点P在射线OC上，Q是OA上一动点，则PA+PQ的最小值是
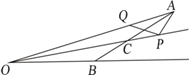18. 如图，△ABC是等边三角形，点P是AB的中点，点M在CB的延长线上，点N在AC上，且满足∠MPN=120°.已知△ABC的周长为12，设m=2AC-CM-CN，若关于 的方程 的解是正数，则 的取值范围是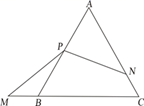
三、解答题
-
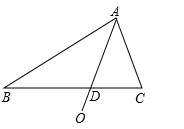
19. 某中学计划为新生配备如图1所示的折叠凳，图2是折叠凳撑开后的侧面示意图（木条等材料宽度忽略不计），其中凳腿AB和CD的长度相等，O是它们的中点，为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为35cm，由以上信息能求出CB的长度吗？如果能，请求出CB的长度；如果不能，请说明理由.
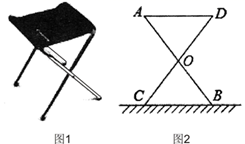20. 已知一个n边形的每个内角是135º.(1)、求n；(2)、求这个n边形的内角和.21. 如图，在边长为1个单位长度的小正方组成的网格中，按要求画出△A1B1C1与△A2B2C2.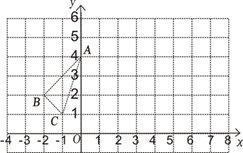
（ 1 ）作出△ABC关于y轴对称的△A1B1C1；
（ 2 ）将△ABC向右平移6个单位，作出平移后的△A2B2C2；
（ 3 ）观察△A1B1C1和△A2B2C2 ， 他们是否关于某直线对称？若是，请用粗线条画出对称轴.
22. 若 是△ABC的两边且(1)、试求 的值，并求第三边 的取值范围.(2)、若△ABC是等腰三角形，试求此三角形的周长.(3)、若另一等腰三角形DEF，其中一个内角为x°，另一个内角为(2x-20)°，试求此三角形的各内角度数.23. 如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D ， BC=CE ．
(1)、求证：AC=CD；(2)、若AC=AE ， 求∠DEC的度数．24. 如图所示，在△ABC中，AB＝AC＝20cm，BC＝16cm，D为AB中点，如果点P在线段BC上由点B出发向点C运动，同时点Q在线段CA上由点C出发向点A运动，设运动时间为t（s）.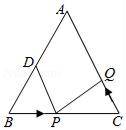
(1)、若点P与点Q的速度都是2cm/s，问经过多少时间△BPD与△CQP全等？说明理由；(2)、若点P的速度比点Q的速度都慢2cm/s，则经过多少时间△BPD与△CQP全等，并求出此时两点的速度；(3)、若点P、点Q分别以（2）中速度同时从B、C出发，都逆时针沿△ABC三边运动，问经过多少时间点P与点Q第一次相遇，相遇点在△ABC的哪条边上？并求出相遇点与点B的距离.25. 如图1，在△ABC中，∠ACB=2∠B，∠BAC的平分线AO交BC于点D，点H为AO上一动点，过点H作直线l⊥AO于H，分别交直线AB、AC、BC、于点N、E、M．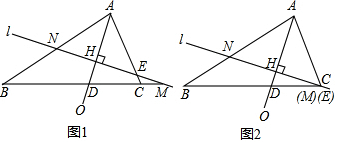
(1)、当直线l经过点C时（如图2），求证：BN=CD；(2)、当M是BC中点时，写出CE和CD之间的等量关系，并加以证明；(3)、请直接写出BN、CE、CD之间的等量关系．