广西桂林市灌阳县2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x - 2}{x + 1} = 0$ ，x则等于（）

A、0 B、-2 C、-1 D、2

查看试题解析
2. 以下列各组长度的线段为边，能构成三角形的是（）

A、7，3，4 B、5，6，12 C、3，4，5 D、1，2，3

查看试题解析
3. 下列各式： $\frac{a - b}{2}$ ， $\frac{x + 3}{x}$ ， $\frac{1}{3}$ ， $\frac{a + b}{a - b}$ ， $\frac{1}{m} (x - y)$ 中，是分式的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 计算： $2^{- 1} =$ （）

A、2 B、- 2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
5. 如图1，将三角板的直角顶点放在直角尺的一边上，∠1=30°，∠2=50°，则∠3的度数为（）

A、80° B、50° C、30° D、20°

查看试题解析
6. 下列说法正确的有几个（）
①2020⁰=1；②三个角分别相等的两个三角形是全等三角形；③分式的分母为0，则分式的值不存在；④若 $b \neq 0$ 那么 $\frac{c}{a} = \frac{c b}{a b}$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，AB∥DE，AF=DC，若要证明△ABC≌△DEF，还需补充的条件是（）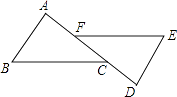

A、AC=DF B、AB=DE C、∠A=∠D D、BC=EF

查看试题解析
8. 某农场开挖一条480m的渠道，开工后，每天比原计划多挖20m，结果提前4天完成任务，若设原计划每天挖xm，那么所列方程正确的是（）

A、 $\frac{480}{x + 20} - \frac{480}{x}$ = 4 B、 $\frac{480}{x} - \frac{480}{x + 4}$ = 20 C、 $\frac{480}{x} - \frac{480}{x + 20}$ = 4 D、 $\frac{480}{x - 4} - \frac{480}{x}$ = 20

查看试题解析
9. 若等腰三角形的两边长为8cm、3cm，则第三边长为（）

A、3cm B、11cm C、8cm或3cm D、8cm

查看试题解析
10. 如果把分式 $\frac{x + y}{xy}$ 中的 $x 、 y$ 都扩大2倍，那么分式的值（）

A、不变 B、缩小2倍 C、扩大2倍 D、无法确定

查看试题解析
11. 若分式方程 $\frac{1}{x - 2} + 3 = \frac{a - x}{x - 2}$ 有增根，则a的值是（）

A、1 B、0 C、-1 D、3

查看试题解析
12. 如图，已知长方形ABCD，将△DBC沿BD折叠得到△DBC′，BC′与AD交于点E，若长方形的周长为20cm，则△ABE的周长是（）

A、5cm B、10cm C、15cm D、20cm

查看试题解析

二、填空题

13. 计算： $a^{2} \cdot a^{3} =$ .

查看试题解析
14. 用科学记数法表示：-0.00000202=.

查看试题解析
15. 如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=12，CF=3，则AC =.

查看试题解析
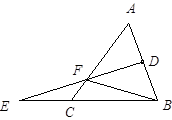16. 命题：“如果a = b ，那么a²=b²”的逆命题是命题（填“真”或“假”）

查看试题解析
17. 若三角形其中两边的长是11和6，则第三边x的取值范围是.

查看试题解析
18. 如图，已知∠MON＝30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄ ， …均为等边三角形，若OA₁＝1，则△A₆B₆A₇的边长为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- \frac{1}{2})}^{- 1} - 2^{5} \div 2^{3} + {(π - 3.14 + 2020)}^{0}$

(2)、 $\frac{m^{2} - m}{m^{2} - 2 m + 1} \div \frac{2}{m - 1} - m$

查看试题解析
20. 解下列分式方程：

(1)、 $\frac{3}{x - 1} = \frac{2}{x - 1} + 1$ ；

(2)、 $\frac{5}{x - 2} - \frac{3}{x^{2} - 4} = \frac{1}{2 - x}$

查看试题解析
21. 如图，△ABC中，AB = AC，∠A = 36°，AC的垂直平分线交AB于E，ED⊥AC，D为垂足，连接EC.

(1)、求∠ECD的度数；

(2)、若CE = 8，求BC长.

查看试题解析
22. 先化简，再求值： $(\frac{2}{x + 1} - \frac{2 x - 3}{x^{2} - 1}) \div \frac{1}{x + 1}$ ，其中 $| x | = 3$ .

查看试题解析
23. 已知：如图，在△ABC中，AB = AC，点D是BC的中点，作∠EAB=∠BAD，AE边交CB的延长线于点E，延长AD到点F，使AF = AE，连结CF.

(1)、求证：BE = CF；

(2)、若∠ACF = 100°，求∠BAD的度数.

查看试题解析
24. 如图，△ABC中，AB＝AC，AB的垂直平分线DE分别交AC、AB于点D、E.

(1)、若∠A＝50°，求∠CBD的度数；

(2)、若AB＝8，△CBD周长为13，求BC的长.

查看试题解析
25. 李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距联欢会开始还有48分钟，于是他立即步行（匀速）回家，在家拿道具用了2分钟，然后立即骑自行车（匀速）返回学校。已知李明骑自行车到学校比他从学校步行到家用时少20分钟，且骑自行车的速度是步行速度的3倍.

(1)、李明步行的速度是多少？

(2)、李明能否在联欢会开始前赶到学校？

查看试题解析
26. 如图

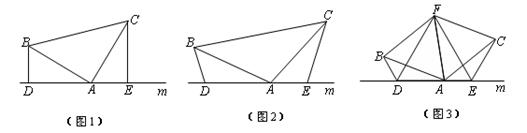(1)、如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E.证明：DE=BD+CE.

(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC= $α$ ，其中 $α$ 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立，请你给出证明；若不成立，请说明理由.

(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

查看试题解析