四川省绵阳市三台县2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-17 类型:期中考试
一、单选题
-
1. 一实验室检测A、B、C、D四个元件的质量(单位:克),超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的元件是( )A、
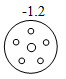 B、
B、 C、
C、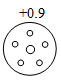 D、
D、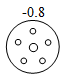 2. 在﹣4, ,0, ,3.14159,0.121121112…这些数中,有理数有( )个.A、5 B、4 C、3 D、23. 下列说法中,正确的是( )A、单项式y的次数是0,系数也是0 B、单项式 的系数是-5,次数是3 C、-5是次数为1的单项式 D、单项式2 x2y的系数是2 ,次数是34. 下面计算正确的是( )A、3a+6b=9ab B、3a3b-3ba3=0 C、8a4-6a3=2a D、 y2- y2=5. 煤层气是优质清洁能源,据报道,截至2019年12月31日,山西省全年煤层气地面抽采量达到56.57亿m3 , 创历史新高,其中利用量为53.94亿m3 , 约占全国的90%.全国煤层气利用量用科学记数法可表示为( )A、59.93×108m3 B、5.993×109m3 C、5.394×109m3 D、5.657×109m36. 下列运用等式的性质对等式进行的变形中,错误的是( )A、若a=b,则 B、若a=b,则ac=bc C、若a(x2+1)=b(x2+1),则a=b D、若x=y,则x﹣3=y﹣37. 下列方程的解是 的有( )
2. 在﹣4, ,0, ,3.14159,0.121121112…这些数中,有理数有( )个.A、5 B、4 C、3 D、23. 下列说法中,正确的是( )A、单项式y的次数是0,系数也是0 B、单项式 的系数是-5,次数是3 C、-5是次数为1的单项式 D、单项式2 x2y的系数是2 ,次数是34. 下面计算正确的是( )A、3a+6b=9ab B、3a3b-3ba3=0 C、8a4-6a3=2a D、 y2- y2=5. 煤层气是优质清洁能源,据报道,截至2019年12月31日,山西省全年煤层气地面抽采量达到56.57亿m3 , 创历史新高,其中利用量为53.94亿m3 , 约占全国的90%.全国煤层气利用量用科学记数法可表示为( )A、59.93×108m3 B、5.993×109m3 C、5.394×109m3 D、5.657×109m36. 下列运用等式的性质对等式进行的变形中,错误的是( )A、若a=b,则 B、若a=b,则ac=bc C、若a(x2+1)=b(x2+1),则a=b D、若x=y,则x﹣3=y﹣37. 下列方程的解是 的有( )① ② ③ ④
A、1个 B、2个 C、3 D、4个8. 已知a、b为有理数,且a<0,b>0,|b|<|a|,则a,b,﹣a,﹣b的大小关系是( )A、﹣b<a<b<﹣a B、﹣b<b<﹣a<a C、a<﹣b<b<﹣a D、﹣a<b<﹣b<a9. 若单项式 ,那么( )A、 B、 C、 D、10. 下列各式去括号正确的是( )A、a﹣(a﹣b+c)=a﹣a+b+c B、a﹣[﹣(﹣b﹣c)]=a﹣b﹣c C、(x+y)﹣(x﹣y)=2x﹣2y D、(x﹣y)﹣(y﹣x)=011. 按如图所示的运算程序,能使输出y值为1的是( ) A、m=﹣1,n=1 B、m=1,n=0 C、m=1,n=2 D、m=2,n=112. 已知数 的大小关系如图,下列说法:
A、m=﹣1,n=1 B、m=1,n=0 C、m=1,n=2 D、m=2,n=112. 已知数 的大小关系如图,下列说法:
① ab+ac>0 ;②-a-b+c>0;③ ④ |a-b|-|c+b|+|a-c|=-2b.其中正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
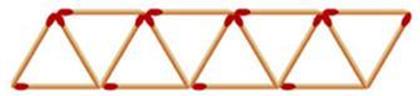
13. 的相反数是.14. 下列说法:①﹣a一定是负数;②|a|=|b|,那么a=b;③倒数等于它本身的数是±1;④绝对值等于它本身的数是0;⑤平方等于它本身的数是1.其中正确的是 . (填序号)15. 多项式 是关于 的四次三项式,则 的值是 .16. 两艘船从同一港口出发,甲船顺水而下,乙船逆水而上,已知两船在静水中的速度都是50km/h,水流速度是 km/h. 则2h后两船相距千米.17. 如果 ,那么代数式 的值是 .18. 如图,用火柴棍拼成一排由三角形组成的图形,如果图形中含有n个三角形,则需要根火柴棍。
三、解答题
-
19. 计算(1)、|8﹣35|﹣( )÷(2)、﹣14+〔1﹣(1﹣0.5×2)〕÷|2﹣(﹣3)2|20. 规定 是一种新的运算法则,满足: .示例: .(1)、求 的值;(2)、若 ,求 的值.21. 已知代数式A=x2+xy﹣2y , B=2x2﹣2xy+x﹣1.(1)、求2A﹣B;(2)、若2A﹣B的值与x的取值无关,求y的值.(3)、在(2)的条件下,求出原式的值.22. 小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
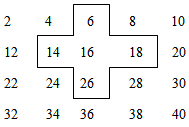 (1)、设中间的数为x , 用代数式表示十字框中的五个数的和;(2)、若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2016吗?如能,写出这五个数,如不能,说明理由.23. 某学校准备在网上为学校定购一批某品牌足球和跳绳,在查阅网店后发现足球每个定价140元,跳绳每条定价30元,现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案,A网店:买一个足球送一条跳绳;B网店:足球和跳绳都按定价的90%付款.
(1)、设中间的数为x , 用代数式表示十字框中的五个数的和;(2)、若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2016吗?如能,写出这五个数,如不能,说明理由.23. 某学校准备在网上为学校定购一批某品牌足球和跳绳,在查阅网店后发现足球每个定价140元,跳绳每条定价30元,现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案,A网店:买一个足球送一条跳绳;B网店:足球和跳绳都按定价的90%付款.已知要购买足球60个,跳绳x根(x > 60).
(1)、若在A网店购买,需付款元.(用含x的代数式表示);若在B网店购买,需付款元.(用含x的代数式表示)(2)、若 时,通过计算说明此时在哪家网店购买较为划算?(3)、当 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?24. 已知:数轴上A、B两点表示的有理数为a、b,且(a﹣1)2+|b+2|=0.(1)、A、B各表示哪一个有理数?(2)、点C在数轴上表示的数是c,且与A、B两点的距离和为11,求多项式a(bc+3)﹣ c2﹣3(a﹣ c2)的值;(3)、小蚂蚁甲以1个单位长度/秒的速度从点B出发向其左边6个单位长度处的一颗饭粒爬去,3秒后位于点A的小蚂蚁乙收到它的信号,以2个单位长度/秒的速度也迅速爬向饭粒,小蚂蚁甲到达后背着饭粒立即返回,与小蚂蚁乙在数轴上D点相遇,则点D表示的有理数是什么?从出发到此时,小蚂蚁甲共用去多少时间?