四川省成都邛崃市2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2020-12-17 类型：期中考试

进入出卷网下载

一、单选题

1. 如果一个物体向右移动2米记作移动+2米，那么这个物体又移动了-2米的意思是（）

A、物体又向右移动了2米 B、物体又向右移动了4米 C、物体又向左移动了2米 D、物体又向左移动了4米

查看试题解析
2. 新冠状病毒疫情发生以来，截止2月5日全国红十字会共接收社会捐赠款物约6.5993×10⁹元．数据6.5993×10⁹可以表示为（）

A、0.65993亿 B、6.5993亿 C、65.993亿 D、659.93亿

查看试题解析
3. 下列各式正确的是（）

A、 $- | - 5 | = 5$ B、 $- (- 5) = - 5$ C、 $| - 5 | = - 5$ D、 $- (- 5) = 5$

查看试题解析
4. 若|x﹣1|+|y+3|＝0，那么（x+1）（y+1）等于（　　）

A、0 B、﹣3 C、﹣6 D、﹣4

查看试题解析
5. 下列代数式中，不是整式的是（）

A、 $\frac{x + 1}{2}$ B、3 C、 $\frac{1}{a}$ D、a+b

查看试题解析
6. 某商品原价每件 $x$ 元，后来店主将每件增加10元，再降价25%，则现在的单价是（）

A、 $(25 % x + 10)$ 元 B、 $((1 - 25 %) x + 10)$ 元 C、 $25 % (x + 10)$ 元 D、 $(1 - 25 %) (x + 10)$ 元

查看试题解析
7. 如图，面积为27的五边形和面积为22的四边形有部分重叠放在一起，若两个阴影部分的面积分别为 $a 、 b (a > b) ，$ 则a-b的值为（）

A、5 B、4 C、3 D、2

查看试题解析
8. 如果代数式x²﹣3x的值为﹣6，那么代数式3x²﹣9x+5的值为（）

A、3 B、﹣13 C、3或﹣13 D、不能确定

查看试题解析
9. 一组按规律排列的多项式：a+b， $a^{2} - b^{3}$ ， $a^{3} + b^{5}$ ， $a^{4} - b^{7}$ ，……，其中第10个式子的次数是（）

A、10 B、17 C、19 D、21

查看试题解析
10. 墨尔本与北京的时差是+3小时（即同一时刻墨尔本时间比北京时间早3小时），班机从墨尔本飞到北京需用12小时，若乘坐从墨尔本8：00（当地时间）起飞的航班，到达北京机场时，当地时间是（）

A、15：00 B、17：00 C、20：00 D、23：00

查看试题解析

二、填空题

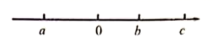
11. 绝对值不大于3的非正整数是.

查看试题解析
12. 有理数 $a$ ， $b$ ， $c$ 在数轴上的对应点如图所示，化简： $| a + b | - | b - c | + | c - a - b | =$ ．

查看试题解析
13. 庆祝中华人民共和国成立70周年大阅兵于2019年10月l日在北京天安门广场举行.通常提到的“阅兵”实际分为“阅兵式”和“分列式”.阅兵式就是士兵不动，军委主席检阅.分列式就是所有方（梯）队，踏着整齐的节奏，依次通过天安门前检阅区，这也是最振奋人心的时刻，在分列式中，受检阅的距离就是天安门前东、西两个华表之间，已知通过这段距离需要68秒，每一正步75厘米，步速每分钟n步，请用含n的代数式表示东西两个华表之间的距离米（要求写最简形式）；

查看试题解析
14. 若多项式 $x y^{| m - n |} + (n - 2) x^{2} y^{2} + 1$ 是关于x，y的三次多项式，则 $m n =$ ．

查看试题解析
15. 绝对值小于4而不小于1的正整数有．

查看试题解析
16. 小明与小刚规定了一种新运算△：a△b=3a﹣2b．小明计算出2△5=﹣4，请你帮小刚计算2△（﹣5）= ．

查看试题解析
17. 厂家检测甲、乙、丙、丁四个足球的质量，超过标准质量的克数记为正数，不足标准质量的克数记为负数，结果如图所示，其中最接近标准质量的足球是．

查看试题解析
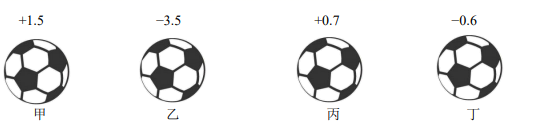18. 图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为 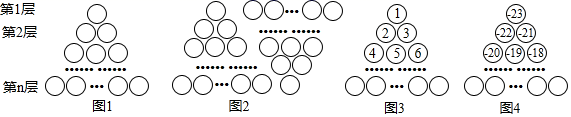$1 + 2 + 3 + \dots + n = \frac{n (n + 1)}{2}$ ．

如果图中的圆圈共有13层，请问：自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1，2，3，4，……，则最底层最左边这个圆圈中的数是；自上往下，在每个圆圈中按图4的方式填上一串连续的整数﹣23，﹣22，﹣21，﹣20，……，则所有圆圈中各数的绝对值之和为．

查看试题解析
19. 为了求1+2+2²+2³+…+2¹⁰⁰的值，可令S＝1+2+2²+2³+…+2¹⁰⁰ ， …①那么2S＝2+2²+2³+…+2¹⁰⁰+2¹⁰¹ ， …②将②﹣①可得2S﹣S＝2¹⁰¹﹣1，所以S＝2¹⁰¹﹣1，即1+2+2²+2³+…+2¹⁰⁰＝2¹⁰¹﹣1．仿照以上方法计算1+a+a²+a³+…+a²⁰¹⁸（a≠0且a≠1）的值是．

查看试题解析

三、解答题

20. 计算：

(1)、 $(- 48) \times (- \frac{1}{2} - \frac{5}{8} + \frac{7}{12})$ ；

(2)、 $- 3^{2} \div {(- 2)}^{2} \times | - 1 \frac{1}{3} | \times 6 + {(- 2)}^{3}$ ．

查看试题解析
21. 把下列各数用数轴上的点表示出来，并用“＜”把它们连接起来．
$- \frac{5}{4} ， - (- 2) ， - 2^{2} ， - | - 3 | ， - {(- 1)}^{2016} ， 4.5$

查看试题解析
22. 先化简,再求值: $3 x^{2} y - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y)] + 3 x y^{2} - x y ，$ 其中 $x = 3 ， y = - \frac{1}{3} .$

查看试题解析
23. 如图所示，a，b，c分别表示数轴上的数，化简：|2﹣b|+|a+c|﹣|b﹣a﹣c|．

查看试题解析
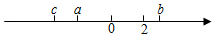24. 已知两个多项式A=9x²y＋7xy－x－2,B=3x²y－5xy＋x＋7

(1)、求A－3B;

(2)、若要使A－3B的值与x的取值无关，试求y的值；

查看试题解析
25. 甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠. 设顾客预计累计购物的费用为x (x＞300)元.

(1)、请用含x的代数式分别表示顾客在两家超市购物所付的费用；

(2)、李明准备购买500元的商品，你认为他应该去哪家超市？请说明理由.

查看试题解析
26. 学校要购入两种记录本，预计花费460元，其中A种记录本每本3元，B种记录本每本2元，且购买A种记录本的数量比B种记录本的2倍还多20本.

(1)、求购买A和B两种记录本的数量；

(2)、某商店搞促销活动，A种记录本按8折销售，B种记录本按9折销售，则学校此次可以节省多少钱？

查看试题解析
27. 阅读并解决问题：归纳
人们通过长期观察发现，如果早晨天空中有棉絮状的高积云，那么午后常有雷雨降临，于是有了“朝有破絮云，午后雷雨临”的谚语.在数学里，我们也常用这样的方法探求规律，例如：三角形有3个顶点，如果在它的内部再画n个点，并以(n+3)个点为顶点，把三角形剪成若干个小三角形，那么最多可以剪得多少个这样的三角形? .为了解决这个问题，我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手，探索最多可以剪得的三角形个数的变化规律.

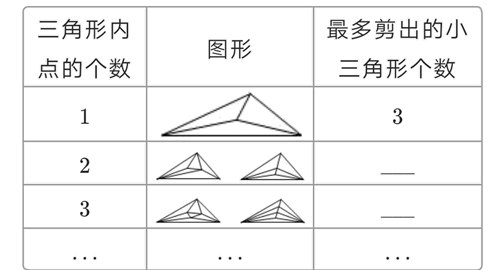(1)、完成表格信息：、；

(2)、通过观察、比较，可以发现：三角形内的点每增加1个，最多可以剪得的三角形增加个.于是，我们可以猜想：当三角形内的点的个数为n时，最多可以剪得个三角形.像这样通过对现象的观察、分析，从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中，人们互相交谈时，常常有人在列举了一些现象后，说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定符合题意，是否符合题意需要加以证实.

(3)、请你借助表格尝试用归纳的方法探索： 1+3+5+7+......+(2n-1)的和是多少?并加以证实.

查看试题解析
28. 如图，数轴上有两定点A、B，点 $A$ 表示的数为6，点B在点A的左侧，且AB=20，动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒（t>0）.

(1)、写出数轴上点B表示的数，点P表示的数用含t的式子表示：；

(2)、设点M是AP的中点，点N是PB的中点.点P在直线AB上运动的过程中，线段MN的长度是否会发生变化？若发生变化，请说明理由；若不变化，求出线段MN的长度.

(3)、动点R从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、R同时出发；当点P运动多少秒时？与点R的距离为2个单位长度.

查看试题解析