浙江省2021年数学学考模拟卷
试卷更新日期:2020-12-17 类型:水平会考
一、单选题
-
1. 已知集合 , ,则 ( )A、{0} B、{1} C、 D、2. 函数 的最小正周期是( )A、 B、 C、 D、3. 计算: ( ).A、5 B、25 C、±5 D、±254. 直线 的倾斜角为( )A、90° B、30° C、0° D、180°5. 函数 的定义域是( )A、 B、 C、 且 D、 且6. 已知空间向量 , ,且 ,则实数 ( )A、 B、-3 C、 D、67. 双曲线 的渐近线方程为( )A、 B、 C、 D、8. 若x,y满足约束条件 ,则 的最大值是( )A、-5 B、1 C、2 D、49. 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )
 A、12 B、36 C、27 D、610. 不等式 的解集为( )A、 B、 C、 D、11. 已知两条直线m,n和平面 ,那么下列命题中的真命题为( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则 或12. 等差数列 的前n项和为 ,若 , ,则当 取得最大值时, ( )A、5 B、6 C、7 D、813. 设a>0且a≠1,则“b>a”是“logab>1”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 已知函数 ,则函数 的定义域为( )A、 B、 C、 D、15. 函数 (其中 为自然对数的底数)的图象大致为( )A、
A、12 B、36 C、27 D、610. 不等式 的解集为( )A、 B、 C、 D、11. 已知两条直线m,n和平面 ,那么下列命题中的真命题为( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则 或12. 等差数列 的前n项和为 ,若 , ,则当 取得最大值时, ( )A、5 B、6 C、7 D、813. 设a>0且a≠1,则“b>a”是“logab>1”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 已知函数 ,则函数 的定义域为( )A、 B、 C、 D、15. 函数 (其中 为自然对数的底数)的图象大致为( )A、 B、
B、 C、
C、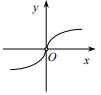 D、
D、 16. 若实数a,b满足 ,则 的最小值为( )A、2 B、3 C、4 D、517. 在一张矩形纸片上,画有一个圆(圆心为O)和一个定点F(F在圆外).在圆上任取一点M,将纸片折叠使M与点F重合,得到折痕CD.设直线CD与直线OM交于点P,则点P的轨迹为( )
16. 若实数a,b满足 ,则 的最小值为( )A、2 B、3 C、4 D、517. 在一张矩形纸片上,画有一个圆(圆心为O)和一个定点F(F在圆外).在圆上任取一点M,将纸片折叠使M与点F重合,得到折痕CD.设直线CD与直线OM交于点P,则点P的轨迹为( )
A、双曲线 B、椭圆 C、圆 D、抛物线18. 在底面为锐角三角形的直三棱柱 中,D是棱 的中点,记直线与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角为 ,则( )
A、 B、 C、 D、二、填空题
-
19. 已知函数 则 , .20. 直线 经过椭圆 的一个焦点和一个顶点,则该椭圆的离心率等于 .21. 已知数列 满足: ,且 ,则 ;22. 已知等腰直角三角形 中, , 顺次为线段 的九等分点,则 的最大值为 .
三、解答题
