山东省临沂市兰山区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-16 类型:期中考试
一、单选题
-
1. 以下关于新型冠状病毒的防范宣传图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
2. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
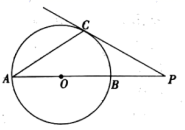
A、1 B、﹣3 C、3 D、43. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ). A、25° B、30° C、35° D、40°4. 用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )A、(x+3)2=1 B、(x﹣3)2=1 C、(x+3)2=19 D、(x﹣3)2=195. 把抛物线 向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为( )A、 B、 C、 D、6. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠17. 若二次函数 的图象经过 , , 三点,则 , , 的大小关系正确的是( )A、 B、 C、 D、8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,在平行四边形 中, ,点 , 在 上,点 在 上, ,则 的度数为( )
A、25° B、30° C、35° D、40°4. 用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )A、(x+3)2=1 B、(x﹣3)2=1 C、(x+3)2=19 D、(x﹣3)2=195. 把抛物线 向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为( )A、 B、 C、 D、6. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠17. 若二次函数 的图象经过 , , 三点,则 , , 的大小关系正确的是( )A、 B、 C、 D、8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,在平行四边形 中, ,点 , 在 上,点 在 上, ,则 的度数为( )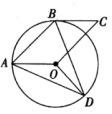 A、112.5° B、120° C、135° D、150°10. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象给出下列结论:
A、112.5° B、120° C、135° D、150°10. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象给出下列结论: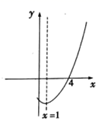
① ;② ;③当 时, 随 的增大而增大;④关于 的一元二次方程 有两个不相等的实数根.其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在平面直角坐标系中,点 与点 关于原点对称,那么m= .12. 1275年,我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.若设长为x步,则可列方程为.13. 已知抛物线 的部分图象如图所示,当 时, 的取值范围是 .
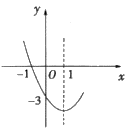 14. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .
14. 我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 . 15. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形 的面积为 ,则 的长为
15. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形 的面积为 ,则 的长为 16. 在 中, , 厘米, 厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过秒后,P,Q两点间距离为 厘米.
16. 在 中, , 厘米, 厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过秒后,P,Q两点间距离为 厘米.
三、解答题
-
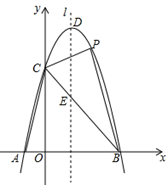
17. 解下列方程:(1)、 ;(2)、 ,18. 在如图所示的平面直角坐标系中(每个小方格都是边长为1个单位长度的正方形),解答下列问题:
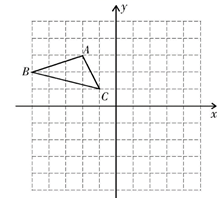 (1)、画出与 关于 轴对称的 ;(2)、画出以C为旋转中心,将 顺时针旋转90°后的 ;(3)、连接 ,则 是三角形,并直接写出 的面积.19. 往直径为 的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽 ,求油的最大深度.
(1)、画出与 关于 轴对称的 ;(2)、画出以C为旋转中心,将 顺时针旋转90°后的 ;(3)、连接 ,则 是三角形,并直接写出 的面积.19. 往直径为 的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽 ,求油的最大深度.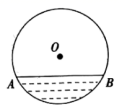 20. 某商店销售一种进价为20元/双的手套,经调查发现,该种手套每天的销售量w(双)与销售单价x(元)满足w=﹣2x+80(20≤x≤40),设销售这种手套每天的利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?
20. 某商店销售一种进价为20元/双的手套,经调查发现,该种手套每天的销售量w(双)与销售单价x(元)满足w=﹣2x+80(20≤x≤40),设销售这种手套每天的利润为y(元).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?