山东省东营市广饶县2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-16 类型:期中考试
一、单选题
-
1. 如图是一个三棱柱笔筒,则该物体的主视图是( )
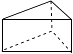 A、
A、 B、
B、 C、
C、 D、
D、 2. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、3. 抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
2. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、3. 抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
A、先向左平移2个单位长度,然后向上平移1个单位长度 B、先向左平移2个单位长度,然后向下平移1个单位长度 C、先向右平移2个单位长度,然后向上平移1个单位长度 D、先向右平移2个单位长度,然后向下平移1个单位长度4. 关于二次函数y=2(x-2)2+5,下列说法错误的是( )A、图象与y轴的交点坐标为(0,13) B、图象的对称轴在y轴的右侧 C、当x>0时,y的值随x值的增大而增大 D、当x=2时,函数有最小值为55. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、6. 下列说法:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.正确的说法有( )A、1个 B、2个 C、3个 D、4个7. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、 B、
B、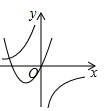 C、
C、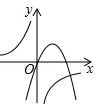 D、
D、 8. 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
8. 如图,△ABC的三个顶点均在格点上,则cosA的值为( )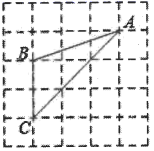 A、 B、 C、2 D、9. 如图,已知二次函数 与一次函数 的图像相交于点A(-3,5),B(7,2),则能使 成立的x的取值范围是( )
A、 B、 C、2 D、9. 如图,已知二次函数 与一次函数 的图像相交于点A(-3,5),B(7,2),则能使 成立的x的取值范围是( ) A、 B、 C、 D、10. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )
A、 B、 C、 D、10. 如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O , 点P是BD上的一个动点,过点P作EF∥AC , 分别交正方形的两条边于点E , F , 连接OE , OF , 设BP=x , △OEF的面积为y , 则能大致反映y与x之间的函数关系的图像为( )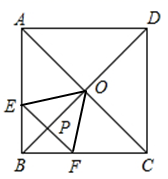 A、
A、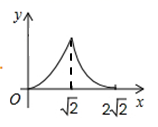 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如果函数 是二次函数,那么m= .12. 若函数 的图象与x轴只有一个公共点,则m的值是 .13. 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为.
 14. 如图,一次函数 与反比例函数 的图像交于 、 两点,其横坐标分别为 和 ,则关于 的不等式 的解集是 .
14. 如图,一次函数 与反比例函数 的图像交于 、 两点,其横坐标分别为 和 ,则关于 的不等式 的解集是 . 15. 一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B处,测得灯塔P在它的东北方向,若灯塔P正南方向4海里的C处是港口,点A,B,C在一条直线上,则这艘货轮由A到B航行的路程为海里(结果保留根号).
15. 一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B处,测得灯塔P在它的东北方向,若灯塔P正南方向4海里的C处是港口,点A,B,C在一条直线上,则这艘货轮由A到B航行的路程为海里(结果保留根号). 16. 将二次函数 的图像沿x轴对折后得到的图像解析式.17. 一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有个碟子.
16. 将二次函数 的图像沿x轴对折后得到的图像解析式.17. 一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有个碟子. 18. 二次函数 的图象如图所示,下列结论:① ;② ;③一元二次方程 有两个不相等的实数根;④当 或 时, .上述结论中正确的是 . (填上所有正确结论的序号)
18. 二次函数 的图象如图所示,下列结论:① ;② ;③一元二次方程 有两个不相等的实数根;④当 或 时, .上述结论中正确的是 . (填上所有正确结论的序号)
三、解答题
-
19. 计算:20. 如图是一个几何体的三视图.
 (1)、写出这个几何体的名称;(2)、求此几何体表面展开图的面积.
(1)、写出这个几何体的名称;(2)、求此几何体表面展开图的面积.
21. 已知在以点 为圆心的两个同心圆中,大圆的弦交小圆于点 、 . (1)、求证: ;(2)、若大圆的半径 ,小圆的半径 ,且圆心 到直线 的距离为 ,求 的长.22. 图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
(1)、求证: ;(2)、若大圆的半径 ,小圆的半径 ,且圆心 到直线 的距离为 ,求 的长.22. 图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)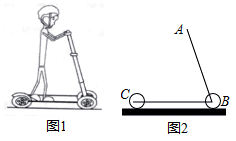 23. 如图,隧道的截面由抛物线和长方形构成.长方形的长为16m , 宽为6m , 抛物线的最高点C离路面AA1的距离为8m .
23. 如图,隧道的截面由抛物线和长方形构成.长方形的长为16m , 宽为6m , 抛物线的最高点C离路面AA1的距离为8m .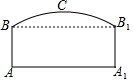 (1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?24. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?25. 如图,抛物线 交x轴于A , B两点,交y轴于点C , 直线BC的表达式为y=-x+3.
(1)、建立适当的坐标系,求出表示抛物线的函数表达式;(2)、一大型货车装载设备后高为7m , 宽为4m . 如果隧道内设双向行驶车道,那么这辆货车能否安全通过?24. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?25. 如图,抛物线 交x轴于A , B两点,交y轴于点C , 直线BC的表达式为y=-x+3. (1)、求抛物线的表达式;(2)、动点D在直线BC上方的二次函数图象上,连接DC , DB , 设△BCD的面积为S , 求S的最大值;(3)、当点D为抛物线的顶点时,在坐标轴上是否存在一点Q , 使得以A , C , Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、动点D在直线BC上方的二次函数图象上,连接DC , DB , 设△BCD的面积为S , 求S的最大值;(3)、当点D为抛物线的顶点时,在坐标轴上是否存在一点Q , 使得以A , C , Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.