内蒙古包头青山区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-16 类型:期中考试
一、单选题
-
1. 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体,它的左视图是( )
 A、
A、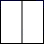 B、
B、 C、
C、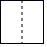 D、
D、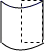 2. 下列函数y是x的反比例函数的是( )A、y=2x B、y= x﹣1 C、y= D、y=﹣x3. 一元二次方程x2﹣x=0的解是( )A、x1=﹣1,x2=0 B、x1=1,x2=0 C、x1=﹣1,x2=1 D、x1=x2=14. 对于线段a,b,如果a:b=2:3,那么下列四个选项一定正确的是( )A、2a=3b B、b﹣a=1 C、 D、5. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、6. 如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
2. 下列函数y是x的反比例函数的是( )A、y=2x B、y= x﹣1 C、y= D、y=﹣x3. 一元二次方程x2﹣x=0的解是( )A、x1=﹣1,x2=0 B、x1=1,x2=0 C、x1=﹣1,x2=1 D、x1=x2=14. 对于线段a,b,如果a:b=2:3,那么下列四个选项一定正确的是( )A、2a=3b B、b﹣a=1 C、 D、5. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、6. 如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( ) A、③—④—①—② B、②—①—④—③ C、④—①—②—③ D、④—①—③—②7. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( )
A、③—④—①—② B、②—①—④—③ C、④—①—②—③ D、④—①—③—②7. 如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为( ) A、105° B、115° C、125° D、135°8. 某口罩加工厂今年一月口罩产值达80万元,第一季度总产值达340万元,问二,三月份的月平均增长率是多少?设月平均增长率的百分数为x,则由题意可得方程为( )A、80(1+x)2=340 B、80+80(1+x)2=340 C、80(1+x)+80(1+x)2=340 D、80+80(1+x)+80(1+x)2=3409. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )
A、105° B、115° C、125° D、135°8. 某口罩加工厂今年一月口罩产值达80万元,第一季度总产值达340万元,问二,三月份的月平均增长率是多少?设月平均增长率的百分数为x,则由题意可得方程为( )A、80(1+x)2=340 B、80+80(1+x)2=340 C、80(1+x)+80(1+x)2=340 D、80+80(1+x)+80(1+x)2=3409. 如图所示,在▱ABCD.BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形有( )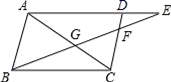 A、3对 B、4对 C、5对 D、6对10. 如图,函数 与 在同一平面直角坐标系中的图像大致( )A、
A、3对 B、4对 C、5对 D、6对10. 如图,函数 与 在同一平面直角坐标系中的图像大致( )A、 B、
B、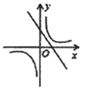 C、
C、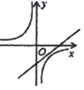 D、
D、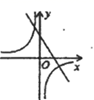 11. 如图,在平行四边形 .点 在边 上, ,连接 交 于点 ,则 的面积与 的面积之比为( )
11. 如图,在平行四边形 .点 在边 上, ,连接 交 于点 ,则 的面积与 的面积之比为( ) A、9:16 B、3:4 C、9:4 D、3:212. 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高为1.5米,那么路灯A的高度AB是( )
A、9:16 B、3:4 C、9:4 D、3:212. 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高为1.5米,那么路灯A的高度AB是( ) A、4.5米 B、6米 C、7.2米 D、8米
A、4.5米 B、6米 C、7.2米 D、8米二、填空题
-
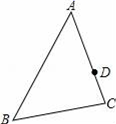
13. 反比例函数y= 图象的每一条曲线上,y随x的增大而减小,则k的取值范围是 .14. 已知一元二次方程x2﹣3x﹣1=0的两个根是x1、x2 , 则x1x2= , x1+x2= , = .15. 一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是.16. 若关于x的方程x2+2(k﹣1)x+k2=0有两个不等实根,则k的取值范围是 .17. 如图,已知△ABC.D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.
 18. 已知(-2,y1),(-1,y2),(3,y3)是反比例函数y=- 的图象上的三个点,则y1 , y2 , y3的大小关系是.19. 在一次新年聚会.小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.20. 如图,△ABC、△DCE、△GEF都是正三角形,且B、C、E、F在同一直线上,A、D、G也在同一直线上,设△ABC、△DCE、△GEF的面积分别为S1、S2、S3 . 当S1=4,S2=6时,S3= .
18. 已知(-2,y1),(-1,y2),(3,y3)是反比例函数y=- 的图象上的三个点,则y1 , y2 , y3的大小关系是.19. 在一次新年聚会.小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.20. 如图,△ABC、△DCE、△GEF都是正三角形,且B、C、E、F在同一直线上,A、D、G也在同一直线上,设△ABC、△DCE、△GEF的面积分别为S1、S2、S3 . 当S1=4,S2=6时,S3= .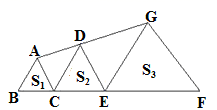
三、解答题
-
21. 解方程:(1)、2x2﹣ x﹣1=0(2)、3(x﹣3)2=4(x﹣3)22. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A,B两点,与x轴交于点P,过点A作AE⊥x轴于点E,AE=3.
 (1)、求点A的坐标;(2)、若PA:PB=3:1,求一次函数的解析式.23. 如图,在平面直角坐标系.△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度).
(1)、求点A的坐标;(2)、若PA:PB=3:1,求一次函数的解析式.23. 如图,在平面直角坐标系.△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度). (1)、将△OAB向右平移1个单位后得到△O1A1B1 , 请画出△O1A1B1;(2)、请以O为位似中心画出△O1A1B1的位似图形,使它与△O1A1B1的相似比为2:1;(3)、点P(a , b)为△OAB内一点,请直接写出位似变换后的对应点P′的坐标为24. 商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?25. 如图①是一张长为18 ,宽为12 的长方形硬纸板,把它的四个角都剪去一个边长为 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)、将△OAB向右平移1个单位后得到△O1A1B1 , 请画出△O1A1B1;(2)、请以O为位似中心画出△O1A1B1的位似图形,使它与△O1A1B1的相似比为2:1;(3)、点P(a , b)为△OAB内一点,请直接写出位似变换后的对应点P′的坐标为24. 商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?25. 如图①是一张长为18 ,宽为12 的长方形硬纸板,把它的四个角都剪去一个边长为 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题: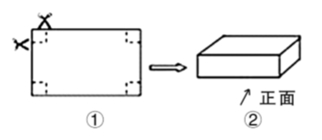 (1)、折成的无盖长方体盒子的容积 ;(用含 的代数式表示即可,不需化简)(2)、请完成下表,并根据表格回答,
(1)、折成的无盖长方体盒子的容积 ;(用含 的代数式表示即可,不需化简)(2)、请完成下表,并根据表格回答,1
2
3
4
5
160
216
80
当 取什么正整数时,长方体盒子的容积最大?
(3)、从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出 的值;如果不是正方形,请说明理由.26. 如图,AD、BE是△ABC的两条高,过点D作DF⊥AB , 垂足为F , FD交BE于M , FD、AC的延长线交于点N . (1)、求证:△BFM∽△NFA;(2)、试探究线段FM、DF、FN之间的数量关系,并证明你的结论;(3)、若AC=BC , DN=12,ME:EN=1:2,求线段AC的长.
(1)、求证:△BFM∽△NFA;(2)、试探究线段FM、DF、FN之间的数量关系,并证明你的结论;(3)、若AC=BC , DN=12,ME:EN=1:2,求线段AC的长.