江西省2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-16 类型:期中考试
一、单选题
-
1. 下列各组长度的线段(单位: )中,成比例线段的是( )A、1,2,3,4 B、1,2,3,5 C、2,3,4,5 D、2,3,4,62. 方程 的解为( )A、 B、 C、 , D、 ,3. 下列各组图形中,一定相似的是( )A、任意两个正方形 B、任意两个平行四边形 C、任意两个菱形 D、任意两个矩形4. 小明制作了5张卡片,上面分别写了一个条件:① ;② ;③ ;④ ,⑤ .从中随机抽取一张卡片,能判定 是菱形的概率为( )A、 B、 C、 D、5. 如图,平行四边形 的对角线 , 相交于点 , 为 的中点,连接 交 于点 ,若 ,则 的长为( )
 A、5 B、6 C、7 D、86. 如图,四边形 是正方形, 是 的中点,连接 与对角线 相交于点 ,连接 并延长,交 于点 ,连接 交 于点 .以下结论:① ;② ;③ ;④ .其中正确结论的个数有( )
A、5 B、6 C、7 D、86. 如图,四边形 是正方形, 是 的中点,连接 与对角线 相交于点 ,连接 并延长,交 于点 ,连接 交 于点 .以下结论:① ;② ;③ ;④ .其中正确结论的个数有( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
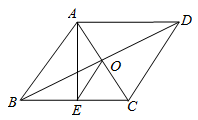
7. 若 ,则 的值为 .8. 在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同,小红通过多次试验发现,摸出红球的频率稳定在0.2左右,则袋子里红球的个数最有可能是 .9. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 .
 10. 若关于 的一元二次方程 的两实数根分别为 , ,且 ,则 的值是 .11. 如图,在矩形 中, , , 是 的黄金分割点( ), 是 上一点,将 沿直线 折叠,点 落在 边上的点 处,再将 沿直线 折叠,点 落在 上的点 处,则 的长为 .
10. 若关于 的一元二次方程 的两实数根分别为 , ,且 ,则 的值是 .11. 如图,在矩形 中, , , 是 的黄金分割点( ), 是 上一点,将 沿直线 折叠,点 落在 边上的点 处,再将 沿直线 折叠,点 落在 上的点 处,则 的长为 .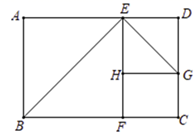 12. 等腰 被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰 的顶角的度数是.
12. 等腰 被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰 的顶角的度数是.三、解答题
-
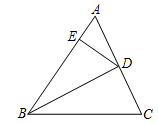
13.(1)、解方程: .(2)、如图,在 中, 平分 ,交 于点 , 是 上一点,连接 ,且 .证明: .
 14. 如图,直线 ,直线 相交于点 ,且分别与直线 相交于点 和点 ,已知 , , , ,求 的长度.
14. 如图,直线 ,直线 相交于点 ,且分别与直线 相交于点 和点 ,已知 , , , ,求 的长度.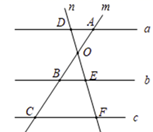 15. 如图,在矩形 中,对角线 , 相交于点 , 于点 , 于点 .
15. 如图,在矩形 中,对角线 , 相交于点 , 于点 , 于点 .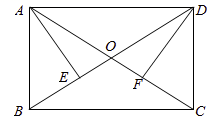 (1)、求证: .(2)、若 ,求 的度数.16. 为答谢全国人民的真情关爱,从8月8日开始,湖北举办“与爱同行惠游湖北”活动,湖北近400家 级旅游景区对全国游客免门票开放.已知A、B、C三个景点实行免门票活动,甲、乙都有去旅游的打算.(1)、若甲随机选择一个景点游玩,则甲选择 景点的概率为 .(2)、利用列表或画树状图的方法,求甲、乙两人选择的两个景点不同的概率.17. 已知矩形 , 为 边上靠近点 的三等分点,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
(1)、求证: .(2)、若 ,求 的度数.16. 为答谢全国人民的真情关爱,从8月8日开始,湖北举办“与爱同行惠游湖北”活动,湖北近400家 级旅游景区对全国游客免门票开放.已知A、B、C三个景点实行免门票活动,甲、乙都有去旅游的打算.(1)、若甲随机选择一个景点游玩,则甲选择 景点的概率为 .(2)、利用列表或画树状图的方法,求甲、乙两人选择的两个景点不同的概率.17. 已知矩形 , 为 边上靠近点 的三等分点,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
 (1)、在图1中作出 边上靠近点 的三等分点 .(2)、在图2中作出点 关于直线 的对称点 .18. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个不相等的实数根.(2)、若这个方程的两根分别为 , ,且满足 ,求 的值.19. 网络购物已成为新的消费方式,催生了快递行业的高速发展,某快递公司今年6月份与8月份投递的快递件数分别为10万件和12.1万件,假定每月投递的快递件数的增长率相同.(1)、求该快递公司投递的快递件数的月平均增长率.(2)、如果每个快递小哥平均每月最多可投递0.8万件快递,该公司现有16个快递小哥,请通过计算说明按此快递件数的增长速度,在不增加人手的情况下,该公司能否完成今年9月份的投递任务.20. 如图,在菱形 中, 为对角线 上一点,且 ,连接 .
(1)、在图1中作出 边上靠近点 的三等分点 .(2)、在图2中作出点 关于直线 的对称点 .18. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个不相等的实数根.(2)、若这个方程的两根分别为 , ,且满足 ,求 的值.19. 网络购物已成为新的消费方式,催生了快递行业的高速发展,某快递公司今年6月份与8月份投递的快递件数分别为10万件和12.1万件,假定每月投递的快递件数的增长率相同.(1)、求该快递公司投递的快递件数的月平均增长率.(2)、如果每个快递小哥平均每月最多可投递0.8万件快递,该公司现有16个快递小哥,请通过计算说明按此快递件数的增长速度,在不增加人手的情况下,该公司能否完成今年9月份的投递任务.20. 如图,在菱形 中, 为对角线 上一点,且 ,连接 . (1)、求证: .(2)、当 于点 , 时,求菱形的边长.21. 如图,已知四边形 是菱形,对角线 , 相交于点 , 于点 ,交 于点 ,连接 并延长,交 于点 .
(1)、求证: .(2)、当 于点 , 时,求菱形的边长.21. 如图,已知四边形 是菱形,对角线 , 相交于点 , 于点 ,交 于点 ,连接 并延长,交 于点 . (1)、求证: .(2)、求证: .
(1)、求证: .(2)、求证: .

