福建省龙岩漳平市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-16 类型:期中考试
一、单选题
-
1. 下列选项的图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某校在一次科普知识抢答比赛中,7名选手的得分分别为:8,7,6,5,5,5,4,则这组数据的众数是( )A、5 B、6 C、7 D、83. 一组数据17,35,18,50,36,99的中位数为( )A、18 B、35 C、35.5 D、504. 一元二次方程3x2-x=2的二次项系数、一次项系数和常数项分别是( )A、3,-1,-2 B、3,-1,2 C、-3,1,-2 D、-3,-l,25. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、 = D、(x+3)2=46. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .7. 关于x的一元二次方程kx2+2x+1=0有实数根,则实数k的取值范围是( )A、k≤1 B、k<1 C、k≤1且k≠0 D、k<1且k≠08. 已知某二次函数,当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,则该二次函数的解析式可以是( )A、y=(x+1)2 B、y=2(x-1)2 C、y=-2(x+1)2 D、y=-2(x-1)29. 关于x的二次函数y=﹣2x2+4x+m2+2m , 下列说法正确的是( )A、该二次函数的图象与x轴始终有两个交点 B、当x>0时,y随x的增大而增大 C、当该二次函数的图象经过原点时,m=﹣2 D、该二次函数的顶点的纵坐标无最小值10. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转45°后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为(1,0),那么点 的坐标为( )
2. 某校在一次科普知识抢答比赛中,7名选手的得分分别为:8,7,6,5,5,5,4,则这组数据的众数是( )A、5 B、6 C、7 D、83. 一组数据17,35,18,50,36,99的中位数为( )A、18 B、35 C、35.5 D、504. 一元二次方程3x2-x=2的二次项系数、一次项系数和常数项分别是( )A、3,-1,-2 B、3,-1,2 C、-3,1,-2 D、-3,-l,25. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、 = D、(x+3)2=46. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .7. 关于x的一元二次方程kx2+2x+1=0有实数根,则实数k的取值范围是( )A、k≤1 B、k<1 C、k≤1且k≠0 D、k<1且k≠08. 已知某二次函数,当x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,则该二次函数的解析式可以是( )A、y=(x+1)2 B、y=2(x-1)2 C、y=-2(x+1)2 D、y=-2(x-1)29. 关于x的二次函数y=﹣2x2+4x+m2+2m , 下列说法正确的是( )A、该二次函数的图象与x轴始终有两个交点 B、当x>0时,y随x的增大而增大 C、当该二次函数的图象经过原点时,m=﹣2 D、该二次函数的顶点的纵坐标无最小值10. 如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转45°后得到正方形 ,依此方式,绕点 连续旋转2020次得到正方形 ,如果点 的坐标为(1,0),那么点 的坐标为( )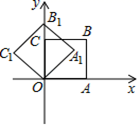 A、(﹣1,1) B、 C、(﹣1,﹣1) D、
A、(﹣1,1) B、 C、(﹣1,﹣1) D、二、填空题
-
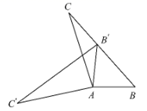
11. 若一组数据1,2,x,4的众数是1,则这组数据的方差为 .12. 平面直角坐标系中,点P(3,1-a)与点Q(b+2,3)关于原点对称,则a+b= .13. 若抛物线 的顶点在 轴的正半轴上,则 的值为.14. 设 是方程 的两个实数根,则 的值是.15. 如图,在 中, ,将 绕点 按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为 .
 16. 设二次函数 的图象顶点为 ,与 轴交点为 、 ,当 为等边三角形时, 的值为 .
16. 设二次函数 的图象顶点为 ,与 轴交点为 、 ,当 为等边三角形时, 的值为 .三、解答题
-
17. 解下列方程:(1)、x2+4x-6=0(用配方法解);(2)、(3x-2)(x+2)=28(用公式法解)18. 已知抛物线y=-(x-1)2+3.
 (1)、抛物线的对称轴是 , 顶点坐标是 .(2)、选取适当的数值填入下表,并在如图所示的直角坐标系中描点画出该抛物线的图像.
(1)、抛物线的对称轴是 , 顶点坐标是 .(2)、选取适当的数值填入下表,并在如图所示的直角坐标系中描点画出该抛物线的图像.…
…
…
…
(3)、说明该抛物线与抛物线y=-x2有什么关系.19. 定义新运算“⊕”如下:当a≥b时,a⊕b=ab-a;当a<b时,a⊕b=ab+a(1)、计算:(-2)⊕( );(2)、若2x⊕(x+1)=8,求x的值20. 如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC , 连接OD , OA .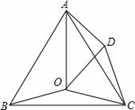 (1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.21. 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
(1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.21. 孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.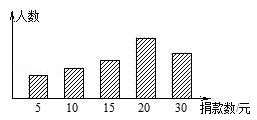 (1)、孔明同学调查的这组学生共有人;(2)、这组数据的众数是元,中位数是元;(3)、若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?22. 已知关于x的一元二次方程 .(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?23. 某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE、EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.
(1)、孔明同学调查的这组学生共有人;(2)、这组数据的众数是元,中位数是元;(3)、若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?22. 已知关于x的一元二次方程 .(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?23. 某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图,BE、EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米. (1)、求出S与x的函数关系式,直接写出自变量x的取值范围;(2)、若矩形ABCD的面积为252平方米,求AB的长.24. 综合与实践
(1)、求出S与x的函数关系式,直接写出自变量x的取值范围;(2)、若矩形ABCD的面积为252平方米,求AB的长.24. 综合与实践问题情境:
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 ),延长 交 于点 ,连接 .
猜想证明:
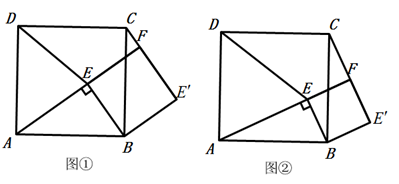 (1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;
(1)、试判断四边形 的形状,并说明理由;(2)、如图②,若 ,请猜想线段 与 的数量关系并加以证明;解决问题:
(3)、如图①,若 , ,请直接写出 的长.25. 已知二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C .(1)、当m≠﹣4时,说明这个二次函数的图象与x轴必有两个交点;(2)、若OA•OB=6,求点C的坐标;(3)、在(2)的条件下,在x轴下方的抛物线上找一点P , 使S△PAC的面积为15,求P点的坐标.