初中数学苏科版八年级上学期期末复习专题(7) 勾股定理的简单应用
试卷更新日期:2020-12-16 类型:复习试卷
一、单选题
-
1. 如图,由于受台风的影响,一颗大树在离地面6 m处折断,顶端落在离树干底部8 m处,则这棵树在折断前的高度是( )
 A、8m B、10m C、16m D、18m2. 已知一轮船以18海里/小时的速度从港口 出发向西南方向航行,另一轮船以24海里/小时的速度同时从港口 出发向东南方向航行,离开港口1.5 后,两轮船相距( )A、30海里 B、35海里 C、40海里 D、45海里3. 如图所示,数轴上点A所表示的数为 ,则 的值是( )
A、8m B、10m C、16m D、18m2. 已知一轮船以18海里/小时的速度从港口 出发向西南方向航行,另一轮船以24海里/小时的速度同时从港口 出发向东南方向航行,离开港口1.5 后,两轮船相距( )A、30海里 B、35海里 C、40海里 D、45海里3. 如图所示,数轴上点A所表示的数为 ,则 的值是( ) A、 B、 C、 D、4. 如图,分别以直角三角形的三边作三个半圆,且 , ,则 等于( )
A、 B、 C、 D、4. 如图,分别以直角三角形的三边作三个半圆,且 , ,则 等于( ) A、60 B、40 C、50 D、705. 如图,圆柱形容器高为18cm,底面周长为32cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好也在杯内壁,离杯上沿2cm与蜂蜜正相对的点A处,则蚂蚁从内壁A处到达内壁B处的最短距离为( )
A、60 B、40 C、50 D、705. 如图,圆柱形容器高为18cm,底面周长为32cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好也在杯内壁,离杯上沿2cm与蜂蜜正相对的点A处,则蚂蚁从内壁A处到达内壁B处的最短距离为( )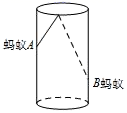 A、13cm B、 cm C、2 cm D、20cm6. 将一根长为25厘米的筷子至于底面直径为5厘米,高为12厘米的圆柱形水杯中,设筷子漏在杯子外的长为h厘米,则h的取值范围是( )A、12≤h≤13 B、11≤h≤12 C、11≤h≤13 D、10≤h≤127. 如图,在 中, , , 的面积是24, 的垂直平分线 分别交 、 边于点 , ,若点 为 边的中点,点 为线段 上一动点,连接 , ,则 的最小值为( )
A、13cm B、 cm C、2 cm D、20cm6. 将一根长为25厘米的筷子至于底面直径为5厘米,高为12厘米的圆柱形水杯中,设筷子漏在杯子外的长为h厘米,则h的取值范围是( )A、12≤h≤13 B、11≤h≤12 C、11≤h≤13 D、10≤h≤127. 如图,在 中, , , 的面积是24, 的垂直平分线 分别交 、 边于点 , ,若点 为 边的中点,点 为线段 上一动点,连接 , ,则 的最小值为( ) A、6 B、10 C、12 D、138. 如图, ,点 为射线 上一点,且 ,点 为 的中点.若点 为射线 上一点,则 的最小值为( )
A、6 B、10 C、12 D、138. 如图, ,点 为射线 上一点,且 ,点 为 的中点.若点 为射线 上一点,则 的最小值为( )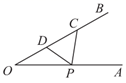 A、2 B、 C、 D、49. 正方形 的边长为1,其面积记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为 ,…按此规律继续下去,则 的值为( )
A、2 B、 C、 D、49. 正方形 的边长为1,其面积记为 ,以 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为 ,…按此规律继续下去,则 的值为( ) A、 B、 C、 D、10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂0A=OB=10分米,晾衣臂支架HG=FE=5分米,HO=FO=4分米。当∠AOC=90°,且OB∥CD时,线段OG与OE的长分别为( )
A、 B、 C、 D、10. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂0A=OB=10分米,晾衣臂支架HG=FE=5分米,HO=FO=4分米。当∠AOC=90°,且OB∥CD时,线段OG与OE的长分别为( )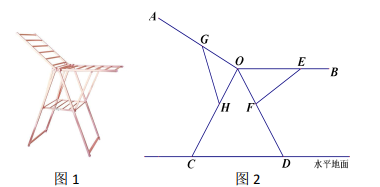 A、3和7 B、3和 C、3和2+ D、 和2+
A、3和7 B、3和 C、3和2+ D、 和2+二、填空题
-
11. 有一块直角三角形绿地,量得两直角边长为6 m,8 m.若现在要将绿地扩充成等腰三角形,且扩充时只能延长6 m的直角边,则扩充后等腰三角形绿地的面积为 m2.12. 如图,有一个三级台阶,它的每一级的长, 宽和高分别是 , , ,点 和点 是这个台阶两个相对的端点, 点有一只蚂蚁,想到 点去吃可口的食物,则蚂蚁沿着台阶表面爬到 点的最短路程是 .
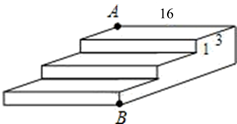 13. 如图Rt△ABC , ∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .
13. 如图Rt△ABC , ∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .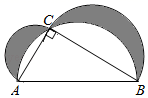 14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的, , ,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长(图中实线部分)是 .
14. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的, , ,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长(图中实线部分)是 . 15. 如图,点A是∠MON=45°内部一点,且OA=4cm,分别在边OM,ON上各取一点B,C,分别连接A,B,C三点组成三角形,则ΔABC最小周长为 。
15. 如图,点A是∠MON=45°内部一点,且OA=4cm,分别在边OM,ON上各取一点B,C,分别连接A,B,C三点组成三角形,则ΔABC最小周长为 。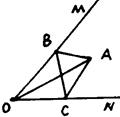 16. 如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 ,已知 ,则 的值是.
16. 如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 ,已知 ,则 的值是.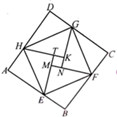 17. 如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .
17. 如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 . 18. 如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+2S2+2S3+S4= .
18. 如图在直线上一次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1+2S2+2S3+S4= .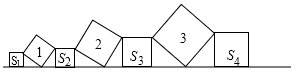
三、解答题
-
19. 如图,某开发区计划在一块四边形的空地ABCD上种植草坪.已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元.求种植草坪的总预算.
 20. (古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
20. (古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题. 21. 《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上行驶速度不得超过70千米/时,一辆小汽车在一条城市街道上直向行驶,某一时刻正好行驶到距车速检测仪 正前方50米的 处,过了6秒后,测得小汽车的位置 与车速检测仪 之间的距离为130米,这辆小汽车超速了吗?请说明理由.
21. 《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上行驶速度不得超过70千米/时,一辆小汽车在一条城市街道上直向行驶,某一时刻正好行驶到距车速检测仪 正前方50米的 处,过了6秒后,测得小汽车的位置 与车速检测仪 之间的距离为130米,这辆小汽车超速了吗?请说明理由. 22. 如图1和图2, 是直线 上一动点, 两点在直线 的同侧,且点 所在直线与 不平行.
22. 如图1和图2, 是直线 上一动点, 两点在直线 的同侧,且点 所在直线与 不平行. (1)、当 点运动到 位置时,距离 点最近,在图1中的直线 上画出点 的位置;(2)、当 点运动到 位置时,与 点的距离和与 点距两相等,请在图2中作出 位置;(3)、在直线 上是否存在这样一点 ,使得到 点的距离与到 点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.
(1)、当 点运动到 位置时,距离 点最近,在图1中的直线 上画出点 的位置;(2)、当 点运动到 位置时,与 点的距离和与 点距两相等,请在图2中作出 位置;(3)、在直线 上是否存在这样一点 ,使得到 点的距离与到 点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.(要求:不写作法,请保留作图痕迹)
23. 如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).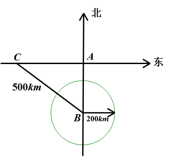 (1)、如果这艘轮船不改变航向,经过11小时,轮船与台风中心相距多远?此时,轮船是否受到台风影响?(2)、如果这艘轮船受到台风影响,请求出轮船受到台风影响一共经历了多少小时?24. 如图:
(1)、如果这艘轮船不改变航向,经过11小时,轮船与台风中心相距多远?此时,轮船是否受到台风影响?(2)、如果这艘轮船受到台风影响,请求出轮船受到台风影响一共经历了多少小时?24. 如图: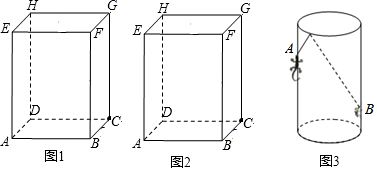 (1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?25. 如图,在公路 的同侧有两个居民点 、 ,居民点 、 分别到公路的距离 千米和 千米,且两个居民点 、 相距 千米.
(1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?25. 如图,在公路 的同侧有两个居民点 、 ,居民点 、 分别到公路的距离 千米和 千米,且两个居民点 、 相距 千米. (1)、要在公路边修一个污水处理站 来收集处理居民点 、 的污水,污水处理站 修在什么地方到居民点 、 所用的水管最短;请你在图中设计出污水处理站 的位置.(保留作图痕迹,不要证明)(2)、如图铺设水管的工程费用为每千米 万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)、要在公路边修一个汽车站 ,使汽车站 到两个居民点 、 的距离相等,则点 应该修在距点 多远的地方(另画图并写出解答过程)26. 认真阅读下列材料,然后完成解答:
(1)、要在公路边修一个污水处理站 来收集处理居民点 、 的污水,污水处理站 修在什么地方到居民点 、 所用的水管最短;请你在图中设计出污水处理站 的位置.(保留作图痕迹,不要证明)(2)、如图铺设水管的工程费用为每千米 万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)、要在公路边修一个汽车站 ,使汽车站 到两个居民点 、 的距离相等,则点 应该修在距点 多远的地方(另画图并写出解答过程)26. 认真阅读下列材料,然后完成解答:(材料)
如图,已知平面直角坐标系中两点A(x1 , y1)、B(x2 , y2),如何求A、B两点间的的距离|AB|的值?
过点A向y轴作垂线AN1、过点B向x轴作垂线BM2 , 垂足分别为N1(0,y1)和M2(x2 , 0),直线AN1和BM2相交于点Q.
在Rt△AQB.|AB|2= |AQ|2+ |BQ|2
为了计算AQ和BQ,过点A向x轴作垂线,垂足为M1(x1 , 0);过点B向y轴作垂线,垂足为N2(0,y2),于是有|AQ|=|M1M2|=|x3-x1|,|BQ|=|N1N2|=|y2-y1|.
所以,|AB|2= .
由此得到A(x1 , y1)、B(x2 , y2)两点间的距离公式: .
根据定义:两点之间线段的长度,叫做这两点之间的距离.
因此,线段AB的长度计算公式为 .
 (1)、(问题)
(1)、(问题)平面直角坐标系中有两点A(0,1)、B(2,3),求线段AB的长;
(2)、 表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为;(3)、如图,在x轴上有一点P(x,0),试求PA+PB的最小值.