初中数学苏科版八年级上学期期末复习专题(6) 勾股定理及勾股定理逆定理
试卷更新日期:2020-12-16 类型:复习试卷
一、单选题
-
1. 下列长度的 3 条线段:
①8,15,17;②4,5,6;③9,12,15;④24,25,7;⑤5,8,17.
其中能构成直角三角形的是( )
A、①②④ B、②④⑤ C、①③⑤ D、①③④ -
2. 如图, 为 的边 上一点,已知 , ,则 的长为( )
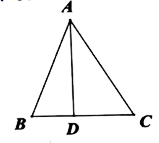 A、13 B、14 C、15 D、16
A、13 B、14 C、15 D、16 -
3. 如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
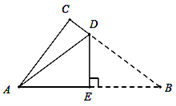 A、4㎝ B、5㎝ C、6㎝ D、 ㎝
A、4㎝ B、5㎝ C、6㎝ D、 ㎝ -
4. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别是9、25、4、9,则最大的正方形E的面积是( )
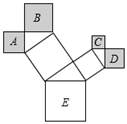 A、13 B、26 C、47 D、94
A、13 B、26 C、47 D、94 -
5. 如图,已知l1∥l2∥l3 , 相邻两条平行直线间的距离均为1,若等腰直角△ABC的三个顶点分别在这三条平行直线上,∠C=90°,求AB的长是( )
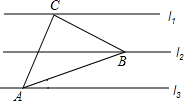 A、3 B、 C、 D、
A、3 B、 C、 D、 -
6. 如图,折叠长方形的一边AD,使点D落在BC边的点F处,若AB=8cm,BC=10cm,则△AEF的面积为( )
 A、40 B、20 C、50 D、25
A、40 B、20 C、50 D、25 -
7. 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN , 则折痕MN的长是( )
 A、5 cm B、5 cm C、4 cm D、4 cm
A、5 cm B、5 cm C、4 cm D、4 cm -
8. 如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1= ;再过点P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2017=( )
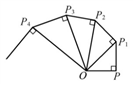 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
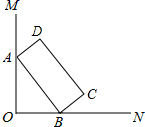 A、 B、 C、 5 D、
A、 B、 C、 5 D、 -
10. 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角,AM=2 EF,则正方形ABCD的面积为( )
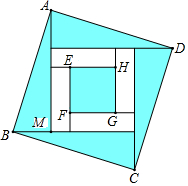 A、14S B、13S C、12S D、11S
A、14S B、13S C、12S D、11S
二、填空题
-
11. △ABC中,如果两条直角边分别为5,12,则斜边上的高线是
-
12. 如图,要为一段高为6米,长为10米的楼梯铺上红地毯,则红地毯至少要米长.

-
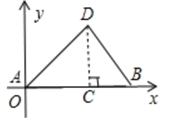
13. 如图,一根橡皮筋放置在x轴上,固定两端A和B,其中A点坐标(0,0),B点坐标(8,0),然后把中点C向上拉升3cm到D,则橡皮筋被拉长了cm.
-
14. 一架长为5米的梯子AB斜立在一竖直的墙上,这时梯子的底端距离C处3米,如果梯子顶端沿墙下滑1米,梯子的底端沿水平方向滑动米.

-
15. 如图,点 是边长为2的等边三角 内任意一点,且 , , ,则 .

-
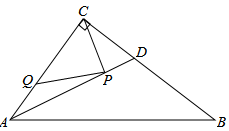
16. 如图,在 中, , , , 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是.
-
17. 在R△ABC中,∠C = 90°,BC = 8 cm,AC = 6 cm,在射线BC上有一动点D从点B出发,以2 cm/s的速度匀速运动,若点D运动(S)时,以点A,D,B为顶点的三角形恰为等腰三角形,则所用时间t为 s.
-
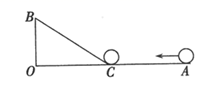
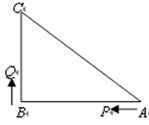
18. 如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为.
三、解答题
-
19. 求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB =3m,BC =12m,CD =13m,DA= 4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?

-
20. 如图,在△ABC中,∠C=90°,AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2 .

-
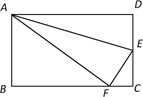
21. 如图,在长方形ABCD(长方形四个角都是直角,并且对边相等)中,DC = 5.点E在DC上,沿AE折叠△ADE , 使D点与BC边上的点F重合,△ABF的面积是30,求DE的长.
-
22. 如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
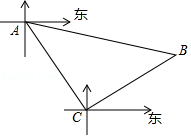 (1)、求此时货轮到小岛B的距离.(2)、在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.
(1)、求此时货轮到小岛B的距离.(2)、在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由. -
23. 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10、OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处。
 (1)、求CE和OD的长;(2)、求直线DE的表达式;(3)、直线y=kx+b与DE平行,当它与长方形OABC有公共点时,直接写出b的取值范围。
(1)、求CE和OD的长;(2)、求直线DE的表达式;(3)、直线y=kx+b与DE平行,当它与长方形OABC有公共点时,直接写出b的取值范围。 -
24. 如图,已知△ABC中,∠B=90 º,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
 (1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
(1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间. -
25. 如图, 为线段 上一动点,分别过点 作 , ,连接 .已知 ,设 .
 (1)、用含 的代数式表示 的值;(2)、探究:当点 满足什么条件时, 的值最小?最小值是多少?(3)、根据(2)中的结论,请构造图形求代数式 的最小值.
(1)、用含 的代数式表示 的值;(2)、探究:当点 满足什么条件时, 的值最小?最小值是多少?(3)、根据(2)中的结论,请构造图形求代数式 的最小值. -
26. 问题探究:(1)、如图①所示是一个半径为 ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形 则蚂蚁爬行的最短路程即为线段 的长)
 (2)、如图②所示是一个底面半径为 ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)、如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
(2)、如图②所示是一个底面半径为 ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)、如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.
