山东省临沂市临沭县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-15 类型:期中考试
一、单选题
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、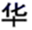 2. 三角形的两边长分别为 和 ,则第三边长可能为( )A、 B、 C、 D、3. 已知正多边形的一个外角等于 ,则这个正多边形的内角和的度数为( )A、 B、 C、 D、4. 如图,将一副三角板按如图所示的方式摆放,其中两条斜边 , 角的顶点与含 角的直角三角板的直角顶点重合,点E,D,C在同一条直线上,则 的为( )
2. 三角形的两边长分别为 和 ,则第三边长可能为( )A、 B、 C、 D、3. 已知正多边形的一个外角等于 ,则这个正多边形的内角和的度数为( )A、 B、 C、 D、4. 如图,将一副三角板按如图所示的方式摆放,其中两条斜边 , 角的顶点与含 角的直角三角板的直角顶点重合,点E,D,C在同一条直线上,则 的为( ) A、 B、 C、 D、5. 如图,等腰△ 中,点D , E分别在腰AB , AC上,添加下列条件,不能判定 ≌ 的是( )
A、 B、 C、 D、5. 如图,等腰△ 中,点D , E分别在腰AB , AC上,添加下列条件,不能判定 ≌ 的是( )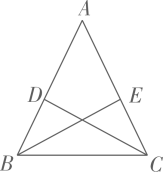 A、 B、 C、 D、6. 下列给出的5个图中,能判定 是等腰三角形的有( )
A、 B、 C、 D、6. 下列给出的5个图中,能判定 是等腰三角形的有( )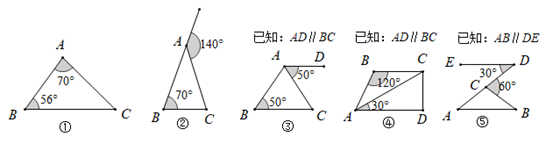 A、2个 B、3个 C、4个 D、5个7. 如图,工人师傅做了一个长方形窗框 ,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )
A、2个 B、3个 C、4个 D、5个7. 如图,工人师傅做了一个长方形窗框 ,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )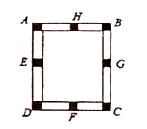 A、E,H两点之间 B、E,G两点之间 C、F,H两点之间 D、A,B两点之间8. 如图,在 中,以点B为圆心, 长为半径画弧,交 边于点D,连接 .若 , ,则 的度数为( )
A、E,H两点之间 B、E,G两点之间 C、F,H两点之间 D、A,B两点之间8. 如图,在 中,以点B为圆心, 长为半径画弧,交 边于点D,连接 .若 , ,则 的度数为( ) A、 B、 C、 D、9. 量角器测角度时摆放的位置如图所示,在 中,射线OC交边AB于点D,则∠ADC的度数为( )
A、 B、 C、 D、9. 量角器测角度时摆放的位置如图所示,在 中,射线OC交边AB于点D,则∠ADC的度数为( ) A、60° B、70° C、80° D、85°10. 如图,A、B、C三岛的平面图,C岛在A岛的北偏东 方向,B岛在A岛的北偏东 方向,C岛在B岛的北偏西 方向,则A、B、C三岛组成的三角形为( )
A、60° B、70° C、80° D、85°10. 如图,A、B、C三岛的平面图,C岛在A岛的北偏东 方向,B岛在A岛的北偏东 方向,C岛在B岛的北偏西 方向,则A、B、C三岛组成的三角形为( )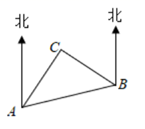 A、等腰直角三角形 B、直角三角形 C、等腰三角形 D、等边三角形11. 在 中, , ,过点B作 ,交 于点D,若 ,则 的长度为( )
A、等腰直角三角形 B、直角三角形 C、等腰三角形 D、等边三角形11. 在 中, , ,过点B作 ,交 于点D,若 ,则 的长度为( ) A、2 B、3 C、4 D、512. 如图,在等腰三角形 中, ,分别以点 为圆心、大于 的长为半径画弧两弧交于点 ,作直线 分别交 于点 ,则线段 与线段 的数量关系是( )
A、2 B、3 C、4 D、512. 如图,在等腰三角形 中, ,分别以点 为圆心、大于 的长为半径画弧两弧交于点 ,作直线 分别交 于点 ,则线段 与线段 的数量关系是( ) A、 B、 C、 D、13. 已知a,b,c为 的三边长b,c满足 ,且a为方程 的解,则 的周长为( )A、6 B、7 C、6或2 D、7或1114. 如图,△ 中, 、 的角平分线 、 交于点 ,延长 、 , , ,则下列结论中正确的个数是( )
A、 B、 C、 D、13. 已知a,b,c为 的三边长b,c满足 ,且a为方程 的解,则 的周长为( )A、6 B、7 C、6或2 D、7或1114. 如图,△ 中, 、 的角平分线 、 交于点 ,延长 、 , , ,则下列结论中正确的个数是( )①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB④若PM⊥BE,PN⊥BC,则AM+CN=AC;
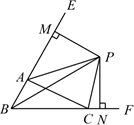 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
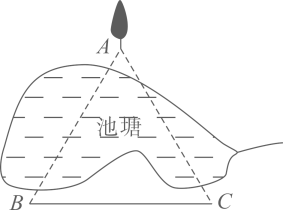
15. 点 关于x轴对称的点的坐标为 .16. 如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置)测得的相关数据为: 米,则 米.
 17. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.
17. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.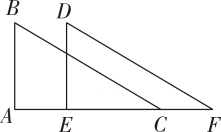 18. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .
18. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .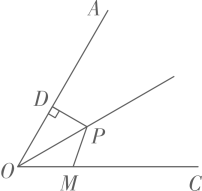 19. 如图,在 中, , ,以点A为圆心,任意长为半径画弧分别交 , 于点M和N,再分别以点M、N为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点D,则下列结论:① 是 的平分线;② ;③点D在 的垂直平分线上;④ .其中结论正确的序号 .
19. 如图,在 中, , ,以点A为圆心,任意长为半径画弧分别交 , 于点M和N,再分别以点M、N为圆心,大于 的长为半径画弧,两弧交于点 ,连接 并延长交 于点D,则下列结论:① 是 的平分线;② ;③点D在 的垂直平分线上;④ .其中结论正确的序号 .
三、解答题
-
20. 如图,已知 ,射线 上一点D.
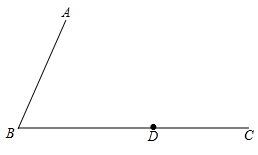
求作:等腰 ,使线段 为等腰 的底边,点P在 内部,且点P到 两边的距离相等.(保留作图痕迹,不必写画法和证明)
21. 如图,在 中, 是 边上的高, , , ,求 的度数.
 22. 如图所示,已知AB//DE,AB=DE,AF=DC,请问图中有哪几对全等三角形?并任选其中一对给予证明.
22. 如图所示,已知AB//DE,AB=DE,AF=DC,请问图中有哪几对全等三角形?并任选其中一对给予证明.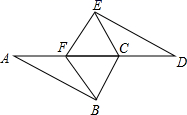 23. 如图, , , , ,
23. 如图, , , , , (1)、求证: ;(2)、试求 的度数.24. 如图:D是 的平分线上一点, , ,垂足分别为M,N.
(1)、求证: ;(2)、试求 的度数.24. 如图:D是 的平分线上一点, , ,垂足分别为M,N.
求证:
(1)、 ;(2)、 .25. 阅读材料:课本中研究图形的性质,就是探究图形的构成元素(边、角、有关线段)具有怎样的特征.例如在学习等腰三角形的性质时,我们就探究得出了等腰三角形有如下性质:
边的性质:等腰三角形两腰相等;
角的性质:等腰三角形的两个底角相等;
有关线段的性质:等腰三角形顶角的平分线、底边上的高、底边的中线是同一条线段.
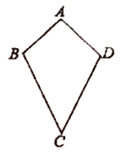
如果两组邻边分别相等的四边形叫筝形.如图,在四边形 ,若 , ,则四边形 是筝形.
请探究筝形的性质,写出两条并进行证明(边的性质除外).
 26. 如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
26. 如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.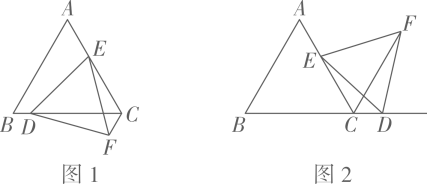 (1)、(问题解决)
(1)、(问题解决)如图1,若点D在边BC上,求证:CE+CF=CD;
(2)、(类比探究)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.