山东省临沂市兰山区2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-15 类型:期中考试
一、单选题
-
1. 在下面的汽车标志图形中,是轴对称图形有( )




 A、1个 B、2个 C、3个 D、4个2. 以下列各组线段为边,不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )
A、1个 B、2个 C、3个 D、4个2. 以下列各组线段为边,不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 如图,△ABC≌△ADE,∠B=70°,∠C=26°,∠DAC=30°,则∠EAC=( )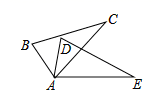 A、27° B、30° C、54° D、55°4. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A、27° B、30° C、54° D、55°4. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )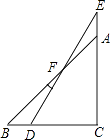 A、15° B、25° C、30° D、10°5. 在数学课上,同学们在练习画边AC上的高时,有一部分同学画出下列四种图形,请你判断一下,正确的是( )A、
A、15° B、25° C、30° D、10°5. 在数学课上,同学们在练习画边AC上的高时,有一部分同学画出下列四种图形,请你判断一下,正确的是( )A、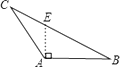 B、
B、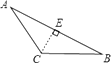 C、
C、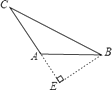 D、
D、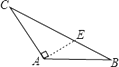 6. 如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
6. 如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )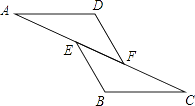 A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC7. 如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).
A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC7. 如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为16,BC=7,则AB的长为( ).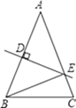 A、8 B、9 C、10 D、118. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )A、7cm B、3cm C、7cm或3cm D、8cm9. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中错误的是()
A、8 B、9 C、10 D、118. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )A、7cm B、3cm C、7cm或3cm D、8cm9. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中错误的是()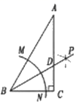 A、BP是∠ABC的平分线 B、AD=BD C、 D、CD= BD10. 如图,在 中, 分别是 , 上的点,作 , ,垂足分别为 ,若 , ,则下列结论:① ;② ;③ ;④ ;⑤ .其中正确的有( )
A、BP是∠ABC的平分线 B、AD=BD C、 D、CD= BD10. 如图,在 中, 分别是 , 上的点,作 , ,垂足分别为 ,若 , ,则下列结论:① ;② ;③ ;④ ;⑤ .其中正确的有( )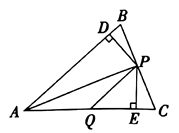 A、①③④ B、①②⑤ C、①②③④ D、①②③④⑤
A、①③④ B、①②⑤ C、①②③④ D、①②③④⑤二、填空题
-
11. 木工师傅做完房门后,为防止变形,会在门上钉上一条斜拉的木条,这样做的根据是 .
 12. 若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画条对角线.13. 如图,在 中, , 平分 , 点在 上, ,若 ,则 .
12. 若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画条对角线.13. 如图,在 中, , 平分 , 点在 上, ,若 ,则 .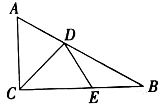 14. 已知点P( )关于x轴的对称点在第一象限,则a的取值范围是15. 如图,在 中, , 平分 , , ,则点D到 的距离是 .
14. 已知点P( )关于x轴的对称点在第一象限,则a的取值范围是15. 如图,在 中, , 平分 , , ,则点D到 的距离是 .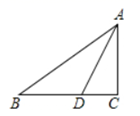 16. 若等腰三角形一腰上的高与另一腰的夹角为 ,腰长为6,则这个等腰三角形的底角度数是 .
16. 若等腰三角形一腰上的高与另一腰的夹角为 ,腰长为6,则这个等腰三角形的底角度数是 .三、解答题
-
17. 如图,在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).
 (1)、在图中作出 关于Y轴对称的 .(2)、写出点 的坐标(直接写答案).(3)、 的面积为.18. 已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.
(1)、在图中作出 关于Y轴对称的 .(2)、写出点 的坐标(直接写答案).(3)、 的面积为.18. 已知:如图,∠BAC=∠DAM,AB=AN,AD=AM,求证:∠B=∠ANM.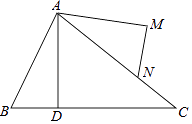 19. 如图,在 中, , 分别是 的高和角平分线,若 , ,求 的度数.
19. 如图,在 中, , 分别是 的高和角平分线,若 , ,求 的度数.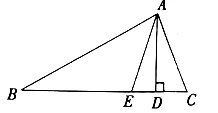 20. 如图,三角形ABC是等边三角形,BD是中线,延长BC至E, 使CE=CD.求证:DB=DE.
20. 如图,三角形ABC是等边三角形,BD是中线,延长BC至E, 使CE=CD.求证:DB=DE.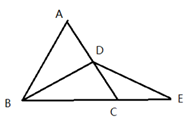 21. 如图,在 中, , 分别是 , 的角平分线.
21. 如图,在 中, , 分别是 , 的角平分线.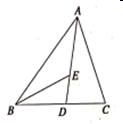 (1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.22.
(1)、若 , ,则 的度数是;(2)、探究 与 的数量关系,并证明你的结论.22.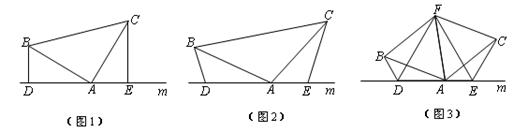 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.