山东省聊城市莘县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-15 类型:期中考试
一、单选题
-
1. 下列4个图案中,既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 如图是两个全等三角形,图中字母表示三角形的边长则 的度数为( )
A、1个 B、2个 C、3个 D、4个2. 如图是两个全等三角形,图中字母表示三角形的边长则 的度数为( )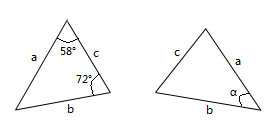 A、50° B、58° C、60° D、70°3. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、4. 已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )A、﹣1 B、1 C、2 D、35. 如图所示,为估计池塘两岸A , B间的距离,一位同学在池塘一侧选取了一点P , 测得PA=16m , PB=12m , 那么A , B间的距离不可能是( )
A、50° B、58° C、60° D、70°3. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、4. 已知点A(2,a)与点B(b,3)关于x轴对称,则a+b的值为( )A、﹣1 B、1 C、2 D、35. 如图所示,为估计池塘两岸A , B间的距离,一位同学在池塘一侧选取了一点P , 测得PA=16m , PB=12m , 那么A , B间的距离不可能是( ) A、15m B、18m C、26m D、30m6. 若 是完全平方式,则m的值是( )A、 B、 C、 或 D、 或7. 已知 是 的两边,且 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、锐角三角形 D、不确定8. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A、15m B、18m C、26m D、30m6. 若 是完全平方式,则m的值是( )A、 B、 C、 或 D、 或7. 已知 是 的两边,且 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、锐角三角形 D、不确定8. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )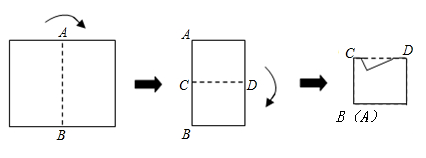 A、
A、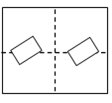 B、
B、 C、
C、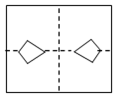 D、
D、 9. 对于以下图形有下列结论,其中正确的是( )
9. 对于以下图形有下列结论,其中正确的是( )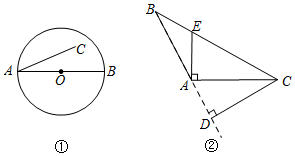 A、如图①, 是弦 B、如图①,直径 与 组成半圆 C、如图②,线段 是 边 上的高 D、如图②,线段 是 边 上的高10. 如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为6,则长方形ABCD的面积为( )
A、如图①, 是弦 B、如图①,直径 与 组成半圆 C、如图②,线段 是 边 上的高 D、如图②,线段 是 边 上的高10. 如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为24,面积之和为6,则长方形ABCD的面积为( )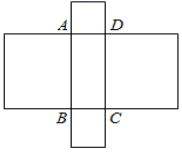 A、4 B、3 C、5 D、611. 如图,大半圆中有n个小半圆,若大半圆弧长为 ,n个小半圆弧长的和为 ,大半圆的弦AB , BC , CD的长度和为 则( )
A、4 B、3 C、5 D、611. 如图,大半圆中有n个小半圆,若大半圆弧长为 ,n个小半圆弧长的和为 ,大半圆的弦AB , BC , CD的长度和为 则( )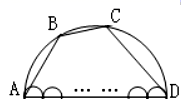 A、 B、 C、无法比较 、 、 间的大小关系 D、12. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )
A、 B、 C、无法比较 、 、 间的大小关系 D、12. 如图,长方形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )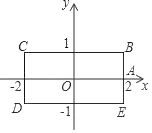 A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)
A、(1,﹣1) B、(2,0) C、(﹣1,1) D、(﹣1,﹣1)二、填空题
-
13. 已知点 .
若点P在x轴上,则点P的坐标为;
若点P在第四象限,且到y轴的距离是2,则点P的坐标为 .
14. 已知等腰三角形的一边等于3cm,一边等于6cm,则它的周长为cm.15. 已知点 , 点的坐标为 ,直线 轴,则a的值是 .16. 如图,在 中, 是 边上的高, 平分 ,若 , ,则 .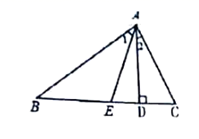 17. 如果 ,那么代数式 的值为 .18. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.
17. 如果 ,那么代数式 的值为 .18. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.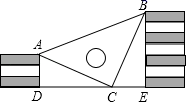
三、解答题
-
19. 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
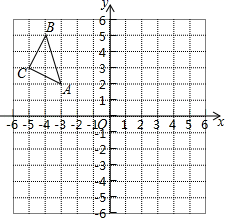 (1)、画出△ABC关于y轴对称的△A1B1C1 , 则点C1的坐标是;(2)、△ABC的面积是多少?20. 因式分解(1)、(2)、21. 先化简再求值: 其中 ,22. 如图,在平面直角坐标系中, 三个顶点的坐标分别为 , , .
(1)、画出△ABC关于y轴对称的△A1B1C1 , 则点C1的坐标是;(2)、△ABC的面积是多少?20. 因式分解(1)、(2)、21. 先化简再求值: 其中 ,22. 如图,在平面直角坐标系中, 三个顶点的坐标分别为 , , .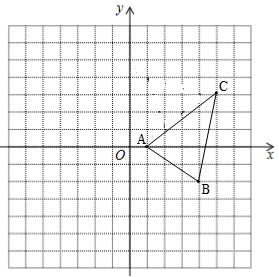 (1)、在图中画出 关于 轴的对称图形 ;(要求:画出三角形,标出相应顶点的字母).(2)、分别写出 三个顶点的坐标并计算 的面积.23. 如图所示, , , 求证: .
(1)、在图中画出 关于 轴的对称图形 ;(要求:画出三角形,标出相应顶点的字母).(2)、分别写出 三个顶点的坐标并计算 的面积.23. 如图所示, , , 求证: .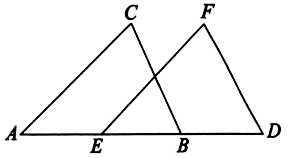 24. 复习“全等三角形”的知识时,老师布置了一道作业题:
24. 复习“全等三角形”的知识时,老师布置了一道作业题: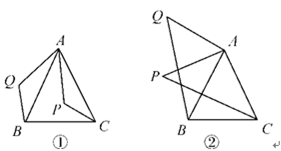
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
25. 如图,在△ABC中,AB=AC , D在边AC上,且BD=DA=BC . (1)、如图1,填空:∠A= .(2)、如图2,若M为线段AC上的点,过M作直线MH⊥BD于H , 分别交直线AB、BC于点N、E .
(1)、如图1,填空:∠A= .(2)、如图2,若M为线段AC上的点,过M作直线MH⊥BD于H , 分别交直线AB、BC于点N、E .①求证:△BNE是等腰三角形;
②试写出线段AN、CE、CD之间的数量关系,并说明理由.