内蒙古包头青山区2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中是最简二次根式的是（）

A、 $\sqrt{4 x}$ B、 $\sqrt{x^{2}}$ C、 $\sqrt{0.5}$ D、 $\sqrt{x^{2} + y^{2}}$

查看试题解析
2. 在0， $3 π$ ， $\sqrt{5}$ ， $\frac{22}{7}$ ， $- \sqrt{9}$ ，6.1010010001…（相邻两个1之间0的个数在递增）中，无理数有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如右图：三个正方形和一个直角三角形，图形A的面积是（）

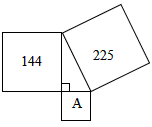A、225 B、144 C、81 D、无法确定

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{{(- 9)}^{2}} = - 9$ B、 $3 \sqrt{2} - 2 \sqrt{2} = 1$ C、 $- 3 \sqrt{5} + \sqrt{5} = - 2 \sqrt{5}$ D、 $- \sqrt{2^{2}} = \sqrt{{(- 2)}^{2}}$

查看试题解析
5. 下列说法正确的有（）
⑴带根号的数都是无理数；

⑵立方根等于本身的数是0和1；

⑶ $- a$ 一定没有平方根；

⑷实数与数轴上的点是一一对应的；

⑸两个无理数的差还是无理数；

⑹若面积为3的正方形的边长为a，a一定是一个无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 某地区用电量与应缴电费之间的关系如下表：则下列叙述错误的是（）

用电量（千瓦•时）

1

2

3

4

…

应缴电费（元）

0.55

1.10

1.65

2.20

…

A、用电量每增加1千瓦•时，电费增加0.55元 B、若用电量为8千瓦•时，则应缴电费4.4元 C、若应缴电费为2.75元，则用电量为6千瓦•时 D、应缴电费随用电量的增加而增加

查看试题解析
7. 如图，将两条边长分别为2和4的长方形如图剪开，拼成一个正方形，则该正方形的边长最接近整数（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，长方形的长为15，宽为10，高为20，点 $B$ 离点 $C$ 的距离为5，蚂蚁如果要沿着长方形的表面从点 $A$ 爬到点 $B$ ，需要爬行的最短距离是（）

A、35 B、 $10 \sqrt{5} + 5$ C、25 D、 $5 \sqrt{21}$

查看试题解析
9. 如图，在平面直角坐标系xOy中，点P(1，0).点P第1次向上跳动1个单位至点P₁(1，1)，紧接着第2次向左跳动2个单位至点P₂(﹣1，1)，第3次向上跳动1个单位至点P₃ ，第4次向右跳动3个单位至点P₄ ，第5次又向上跳动1个单位至点P₅ ，第6次向左跳动4个单位至点P₆ ， ….照此规律，点P第100次跳动至点P₁₀₀的坐标是（）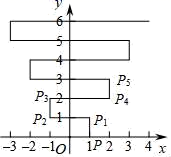

A、(﹣26，50) B、(﹣25，50) C、(26，50) D、(25，50)

查看试题解析
10. 某乡村盛产葡萄，果大味美，甲、乙两个葡萄采摘园为吸引游客，在销售价格一样的基础上分别推出优惠方案，甲采摘园的优惠方案：游客进园需购买门票，采摘的所有葡萄按六折优惠．乙采摘园的优惠方案：游客无需买票，采摘葡萄超过一定数量后，超过的部分打折销售．活动期间，某游客的葡萄采摘量为xkg，若在甲采摘园所需总费用为y_甲元，若在乙采摘园所需总费用为y_乙元，y_甲、y_乙与x之间的函数图象如图所示，则下列说法错误的是（）

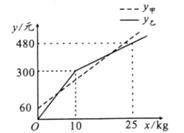A、甲采摘园的门票费用是60元 B、两个采摘园优惠前的葡萄价格是30元/千克 C、乙采摘园超过10kg后，超过的部分价格是12元/千克 D、若游客采摘18kg葡萄，那么到甲或乙两个采摘园的总费用相同

查看试题解析

二、填空题

11. 已知直角三角形两直角边长分别是9、12，则第三边长的值是．

查看试题解析
12. ①12的平方根是；② $\sqrt{64}$ 的立方根是；③ $\frac{\sqrt{3}}{2}$ 的倒数是．

查看试题解析
13. 若一次函数 $y = (2 - m) x + m$ 的图象经过第一，二，三象限，请你写出一个符合上述条件的m的值：．

查看试题解析
14. 已知线段AB的长度为3，且AB平行于y轴，A点坐标为 $(3 ， 2)$ ，则B点坐标为．

查看试题解析
15. 已知：如图，在Rt ∆ABC中， $∠ C = 90^{°}$ ，AB=5cm， AC=3cm，动点P从点B出发沿射线BC以2cm/s 的速度移动，设运动的时间为t秒.t= 时三角形ABP为直角三角形.

查看试题解析
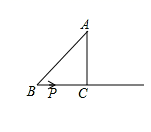16. 在同一直角坐标系中，对于以下四个函数① $y = - x + 1$ ；② $y = x + 1$ ；③ $y = - (x + 1)$ ；④ $y = - 2 (x + 1)$ 的图象，下列说法正确的个数是．
⑴①③④三个函数的图象中，当 $x_{1} > x_{2}$ 时， $y_{1} > y_{2}$ ；

⑵在x轴上交点相同的是②和④；

⑶②中的点到x轴的距离比到y轴的距离都要大1；

⑷函数①和②的图象和x轴围成的图形面积为2．

查看试题解析
17. 疫情之下，中华儿女共抗时艰.重庆和湖北同饮长江水，为更好地驰援武汉，打赢防疫攻坚战，我市某公益组织收集社会捐献物资.甲、乙两人先后从 $A$ 地沿相同路线出发徒步前往 $B$ 地进行物资捐献，甲出发1分钟后乙再出发，一段时间后乙追上甲，这时甲发现有东西落在 $A$ 地，于是原路原速返回 $A$ 地去取（甲取东西的时间忽略不计），而乙继续前行，甲乙两人到达B地后原地帮忙.已知在整个过程中，甲乙均保持各自的速度匀速行走，甲、乙两人相距的路程 $y$ （米）与甲出发的时间 $x$ （分钟）之间的函数关系如图所示，则当乙到达 $B$ 地时，甲距 $A$ 地的路程是米.

查看试题解析

三、解答题

18. 已知点A（a－1，5）和点B（2，b－1）关于x轴对称，求 ${(a + b)}^{2003}$ 的值.

查看试题解析
19.

(1)、 $(\sqrt{48} - \sqrt{27}) \div \sqrt{6}$ ；

(2)、 ${(π - 1)}^{0} - \sqrt[3]{125} + | 1 - \sqrt{3} | + {(- \frac{1}{3})}^{- 2}$ ；

(3)、 $2 (\sqrt{3} - 1) + (5 + \sqrt{6}) (\sqrt{2} - 2 \sqrt{3})$ ；

(4)、已知 $x = \sqrt{3} - 1$ ， $y = \sqrt{3} + 1$ ，求 $x^{2} + x y + y^{2}$ 的值．

查看试题解析
20. 如图，方格纸中每个小方格都是边长为1个单位的正方形，若学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答以下问题：

⑴在图中标出平面直角坐标系的原点，并建立直角坐标系；

⑵若体育馆位置坐标为C（1，﹣3），请在坐标系中标出体育馆的位置；

⑶顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．

查看试题解析
21. 阅读材料，回答问题：

(1)、中国古代数学著作图 $1 《$ 周髀算经 $》$ 有着这样的记载：“勾广三，股修四，经隅五．” $.$ 这句话的意思是：“如果直角三角形两直角边为3和4时，那么斜边的长为 $5.$ ” $.$ 上述记载表明了：在 $Rt △ ABC$ 中，如果 $∠ C = 90 °$ ， $BC = a$ ， $AC = b$ ， $AB = c$ ，那么a，b，c三者之间的数量关系是：．

(2)、对于这个数量关系，我国汉代数学家赵爽根据“赵爽弦图” $($ 如图2，它是由八个全等直角三角形围成的一个正方形 $)$ ，利用面积法进行了证明．参考赵爽的思路，将下面的证明过程补充完整：
证明： $∵ S_{△ ABC =} \frac{1}{2} ab$ ， $S_{正方形 ABCD} = c^{2}$ ，

$S_{正方形 MNPQ} =$ ．

又 $∵$ $=$ ，

$∴ {(a + b)}^{2} = 4 \times \frac{1}{2} ab + c^{2}$ ，

整理得 $a^{2} + 2 ab + b^{2} = 2 ab + c^{2}$ ，

$∴$ ．

(3)、如图3，把矩形ABCD折叠，使点C与点A重合，折痕为EF，如果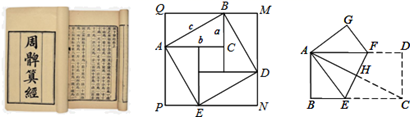 $AB = 4$ ， $BC = 8$ ，求BE的长．

查看试题解析
22. 我们将 $(\sqrt{a} + \sqrt{b})$ 、 $(\sqrt{a} - \sqrt{b})$ 称为一对“对偶式”，因为 $(\sqrt{a} + \sqrt{b}) (\sqrt{a} - \sqrt{b}) = {(\sqrt{a})}^{2} - {(\sqrt{b})}^{2}$ $= a - b$ ，所以构造“对偶式”再将其相乘可以有效的将 $(\sqrt{a} + \sqrt{b})$ 和 $(\sqrt{a} - \sqrt{b})$ 中的“ ”去掉.于是二次根式除法可以这样解：如 $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{2 + \sqrt{2}}{2 - \sqrt{2}} = \frac{{(2 + \sqrt{2})}^{2}}{(2 + \sqrt{2}) \times (2 - \sqrt{2})} = 3 +$ $2 \sqrt{2}$ ．像这样，通过分子，分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化.根据以上材料，理解并运用材料提供的方法，解答以下问题：

(1)、比较大小 $\frac{1}{\sqrt{7} - 2}$ $\frac{1}{\sqrt{6} - \sqrt{3}}$ （用“ $>$ ”、“ $<$ ”或“ $=$ ”填空）；

(2)、已知 $x = \frac{\sqrt{5} + 2}{\sqrt{5} - 2}$ ， $y = \frac{\sqrt{5} - 2}{\sqrt{5} + 2}$ ，求 $x^{2} + y^{2}$ 的值；

(3)、计算： $\frac{2}{3 + \sqrt{3}} + \frac{2}{5 \sqrt{3} + 3 \sqrt{5}} + \frac{2}{7 \sqrt{5} + 5 \sqrt{7}} + \dots \dots + \frac{2}{99 \sqrt{97} + 97 \sqrt{99}}$

查看试题解析
23. 已知正比例函数过点 $A (2 ， - 4)$ ，点P在此正比例函数的图象上，若坐标轴上有一点 $B (0 ， 4)$ 且三角形ABP的面积为8．
求：

(1)、过点A的正比例函数关系式；

(2)、点P的坐标．

查看试题解析

24. 某班“数学兴趣小组”对函数

y = | x + 3 |

的图象和性质进行了探究，探究过程如下，请补充完整．

(1)、自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

x	$\dots$	$- 7$	$- 6$	$- 5$	$- 4$	$- 3$	$- 2$	$- 1$	0	1	$\dots$
y	$\dots$	4	3	m	1	0	1	2	3	4	$\dots$

其中， $m =$ ；

(2)、如图，在平面直角坐标系

x o y

中，描出了以上表格中各对对应值为坐标的点，根据描出的点，请画出函数图象；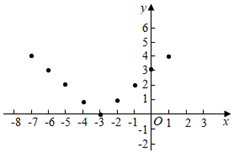

(3)、观察函数图象，写出两条函数图象的性质；；

(4)、进一步探究函数图象发现：

①函数图象与x轴有交点，所以对应的方程 $| x + 3 | = 0$ 有个实数根；

②关于x的方程 $| x + 3 | = a$ 有两个实数根时，a的取值范围是．

查看试题解析

用电量（千瓦•时）	1	2	3	4	…
应缴电费（元）	0.55	1.10	1.65	2.20	…