福建省龙岩漳平市2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2020-12-15 类型：期中考试
一、单选题
-
1. 以下列各组线段为边不能组成三角形的是（ ）A、3，4，4 B、2，6，8 C、2，5，4 D、6，8，102. 下列图形中，为轴对称图形的是（ ）A、
B、
C、
D、
3. 某班同学参加植树，第一组植树15棵，第二组植树18棵，第三组树数14棵，第四组植树19棵．为了把这个班的植树情况清楚地反映出来，应该制作的统计图为（ ）A、条形统计图 B、折线统计图 C、扇形统计图 D、条形统计图、扇形统计图均可4. 点P(5，－4)关于y轴的对称点的坐标是（ ）A、(－5，－4) B、(5，4) C、(－5，4) D、(5，－4)5. 如图所示的图形是轴对称图形，点A和点D，点B和点E是对应点．若∠A＝50°，∠B＝70°，则∠D＋∠E的度数为（ ）
A、100° B、110° C、120° D、130°6. 根据下列条形统计图，下面回答正确的是（ ）
A、步行人数为50人 B、步行与骑自行车的人数和比坐公共汽车的人要少 C、坐公共汽车的人占总数的50% D、步行人最少只有90人7. 如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为（ ）
A、50° B、70° C、75° D、80°8. 如图，OA＝OC，OB＝OD且OA⊥OB，OC⊥OD，下列结论：①△AOD≌△COB；②CD＝AB；③∠CDA＝∠ABC；其中正确的结论是（ ）
A、①② B、①②③ C、①③ D、②③9. 如图，E为 ABC的边AB上一点，AC＝BC＝BE，AE＝EC，BD⊥AC的延长线于点D，则∠CBD的度数为（ ）
A、18° B、28° C、36° D、15°10. 如图，在 ABC中，AB＝AC，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，垂足分别为点E，F，有下列结论：①AD上任意一点到点C，B的距离相等；②AD上任意一点到AB，AC的距离相等；③BD＝CD，AD⊥BC；④∠BDE＝∠CDF．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 2017年11月5日19时45分，我国在西昌卫星发射中心用长征三号乙运载火箭，以“一箭双星”的方式成功发射第二十四、二十五颗北斗导航卫星．这两颗卫星属于中圆地球轨道卫星，是我国北斗三号第一、二颗组网卫星，开启了北斗卫星导航系统全球组网的新时代．如图所示，在发射运载火箭时，运载火箭的发射架被焊接成了许多的三角形，这样做的原因是： ．
12. 某校为了解该校500名毕业生的数学考试成绩，从中抽查了50名考生的数学成绩，在这次调查中，样本是 ．13. 图l是某小区新设置的一款健身器材——双人漫步机，图2是其侧面示意图．在 ABC中，AB＝AC，∠DAB：∠BAC＝9：4，∠B＋∠BAC＝110°，则∠DAC度数为 ．
14. 如图，在△ABC中，DE是BC的垂直平分线，垂足为E，交AC于点D，若AB=6，AC=9，则△ABD的周长是.
15. 如图，∠EOF＝∠OEF＝15°，EF∥OB，EC⊥OB，若OF＝8，则EC等于 ．
16. 已知， ， 的角平分线 和 的角平分线 的反向延长线交于点P ， 且 ，则 度．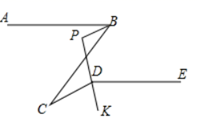
三、解答题
-
17. 如图，点D为码头，A，B两个灯塔与码头的距离相等，DA，DB为海岸线，一轮船离开码头，计划沿∠ADB的平分线航行，在航行途中C点处，测得轮船与灯塔A和灯塔B的距离相等．试问：轮船航行是否偏离指定航线？请说明理由．
18. 如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．
(1)、画出△ABC关于直线BM对称的△A1B1C1；(2)、写出AA1的长度．19. 如图，已知∠BAC=∠BCA，∠BAE=∠BCD=90°，BE=BD．求证：∠E=∠D．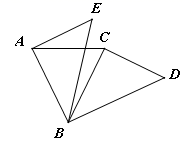
20. 在一个各内角都相等的多边形中，每一个内角都比相邻的外角的3倍还大20°．(1)、求这个多边形的边数．(2)、求这个多边形的内角和及对角线的条数．21. 如图Ⅰ，已知 纸片中， ， ，将其折叠，如图Ⅱ，使点A与点B重合，折痕为 ，点D、E分别在 、 上，求 的大小．
22. 如图，C是BE上一点，D是AC的中点，且AB=AC，DE=DB，∠A=60°，△ABC的周长是18cm．求∠E的度数及CE的长度．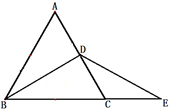
23. 从全校l 200名学生中随机选取一部分学生一周上网时间进行调查，调查情况：A：上网时间≤l小时；B：1小时＜上网时间≤4小时；C：4小时＜上网时间≤7小时；D：上网时间＞7小时．统计结果制成了如下统计图：
(1)、参加调查的学生有人，在扇形统计图中，D类学生所占扇形的圆心角度数为；(2)、请将条形统计图补全；(3)、请估计全校一周上网时间不超过7小时的学生人数．24. 如图，在△ABC中，D是BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连接EG、EF.
(1)、求证：BG＝CF.(2)、求证：EG=EF.(3)、请判断BE+CF与EF的大小关系，并证明你的结论.25. 如图，在△ABC中，∠BAD＝∠DAC，DF⊥AB，DM⊥AC，AF＝10cm，AC＝14cm，动点E以2cm/s的速度从A点向F点运动，动点G以1cm/s的速度从C点向A点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t.
(1)、求证：AF＝AM；(2)、当t取何值时，△DFE与△DMG全等；(3)、求证：在运动过程中，不管t取何值，都有 .