河南省周口市太康县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-15 类型:期末考试
一、单选题
-
1. 若x=﹣1是关于x的一元二次方程ax2﹣bx﹣2019=0的一个解,则1+a+b的值是( )A、2017 B、2018 C、2019 D、20202. 已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )A、3:5 B、9:25 C、5:3 D、25:93. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
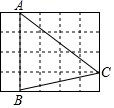 A、 B、 C、 D、4. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )A、 B、 C、 D、5. 抛物线 可由抛物线 如何平移得到的( )A、先向左平移3个单位,再向下平移2个单位 B、先向左平移6个单位,再向上平移7个单位 C、先向上平移2个单位,再向左平移3个单位 D、先回右平移3个单位,再向上平移2个单位6. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A、 B、 C、 D、4. 不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )A、 B、 C、 D、5. 抛物线 可由抛物线 如何平移得到的( )A、先向左平移3个单位,再向下平移2个单位 B、先向左平移6个单位,再向上平移7个单位 C、先向上平移2个单位,再向左平移3个单位 D、先回右平移3个单位,再向上平移2个单位6. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )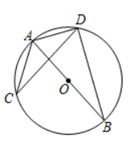 A、 B、 C、 D、7. 已知抛物线 经过 和 两点,则n的值为( )A、﹣2 B、﹣4 C、2 D、48. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).
A、 B、 C、 D、7. 已知抛物线 经过 和 两点,则n的值为( )A、﹣2 B、﹣4 C、2 D、48. 如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( ).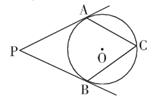 A、60° B、75° C、70° D、65°9. 如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B,与y轴的正半轴交于点C.现有下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正确结论的个数是( )
A、60° B、75° C、70° D、65°9. 如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B,与y轴的正半轴交于点C.现有下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正确结论的个数是( )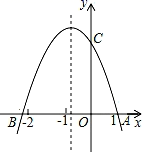 A、1 B、2 C、3 D、410. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
A、1 B、2 C、3 D、410. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在一个不透明的盒子中装有a个除颜色外完全相同的球,其中只有6个白球.若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在20%左右,则a的值约为.12. 如果函数 是关于 的二次函数,则 .13. 若⊙P的半径为5,圆心P的坐标为(﹣3,4),则平面直角坐标系的原点O与⊙P的位置关系是 .14. 已知,点A(-4,y1),B( ,y2)在二次函数y=-x2+2x+c的图象上,则y1与y2的大小关系为.15. 如图,直线 交 轴于点 ,交 轴于点 ,点 是 轴上一动点,以点 为圆心,以1个单位长度为半径作 ,当 与直线 相切时,点 的坐标是 .

三、解答题
-
16. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为.(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.17. 如图,⊙ 中,弦 与 相交于点E, ,连接 .

求证:
(1)、 ;(2)、 .18. 数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55m的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度.(精确到1m.参考数据: , , , )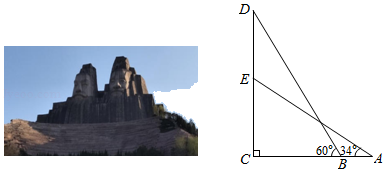 19. 如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B , A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E , 连接BE , 设动点D运动的时间为x(s),AE的长为y(cm).
19. 如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B , A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E , 连接BE , 设动点D运动的时间为x(s),AE的长为y(cm). (1)、求y关于x的函数表达式,并写出自变量x的取值范围;(2)、当x为何值时,△BDE的面积S有最大值?最大值为多少?20. 如图,AB为⊙O的直径,C为⊙O上一点,D为 的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)、求y关于x的函数表达式,并写出自变量x的取值范围;(2)、当x为何值时,△BDE的面积S有最大值?最大值为多少?20. 如图,AB为⊙O的直径,C为⊙O上一点,D为 的中点.过点D作直线AC的垂线,垂足为E,连接OD.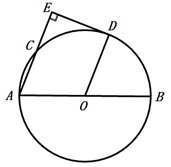 (1)、求证:∠A=∠DOB;(2)、DE与⊙O有怎样的位置关系?请说明理由.21. 小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).(1)、求y与x的函数关系式.(2)、要使日销售利润为720元,销售单价应定为多少元?(3)、求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.22. 如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)、求证:∠A=∠DOB;(2)、DE与⊙O有怎样的位置关系?请说明理由.21. 小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).(1)、求y与x的函数关系式.(2)、要使日销售利润为720元,销售单价应定为多少元?(3)、求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.22. 如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.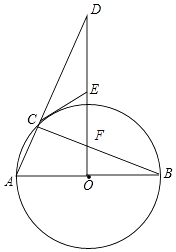 (1)、求证:CE=EF;(2)、连接AF并延长,交⊙O于点G.填空:
(1)、求证:CE=EF;(2)、连接AF并延长,交⊙O于点G.填空:①当∠D的度数为时,四边形ECFG为菱形;
②当∠D的度数为时,四边形ECOG为正方形.
23. 已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.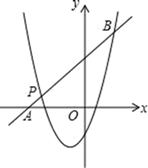 (1)、求m,n的值,(2)、如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,若点B与点M(﹣4,6)关于抛物线对称轴对称,求一次函数的表达式.(3)、根据函数图象直接写出y1>y2时x的取值范围.
(1)、求m,n的值,(2)、如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,若点B与点M(﹣4,6)关于抛物线对称轴对称,求一次函数的表达式.(3)、根据函数图象直接写出y1>y2时x的取值范围.