河南省周口市淮阳区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-15 类型:期末考试
一、单选题
-
1. 要使 有意义,则x的取值范围为( )A、x≤0 B、x≥-1 C、x≥0 D、x≤-12. 下列运算正确的是( )A、 =﹣2 B、(2 )2=6 C、 D、3. 如图,在 中, , , , ,则 的长为( )
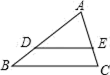 A、6 B、7 C、8 D、94. 已知关于x的一元二次方程 有一个根为 ,则a的值为( )A、0 B、 C、1 D、5. 已知Rt△ABC中,∠C=90º,AC=4,BC=6,那么下列各式中,正确的是( )A、sinA= B、cosA= C、tanA= D、tanB=6. 已知点 P1(a-1,5)和 P2(2,b-1)关于x轴对称,则(a+b)2019的值为( )A、0 B、﹣1 C、1 D、(- 3)20197. 如图,在Rt△ABC中,∠BAC=90º,AH是高,AM是中线,那么在结论①∠B=∠BAM,②∠B=∠MAH,③∠B=∠CAH中错误的个数有( )
A、6 B、7 C、8 D、94. 已知关于x的一元二次方程 有一个根为 ,则a的值为( )A、0 B、 C、1 D、5. 已知Rt△ABC中,∠C=90º,AC=4,BC=6,那么下列各式中,正确的是( )A、sinA= B、cosA= C、tanA= D、tanB=6. 已知点 P1(a-1,5)和 P2(2,b-1)关于x轴对称,则(a+b)2019的值为( )A、0 B、﹣1 C、1 D、(- 3)20197. 如图,在Rt△ABC中,∠BAC=90º,AH是高,AM是中线,那么在结论①∠B=∠BAM,②∠B=∠MAH,③∠B=∠CAH中错误的个数有( )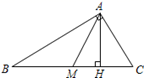 A、0个 B、1个 C、2个 D、3个8. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )
A、0个 B、1个 C、2个 D、3个8. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )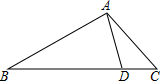 A、 B、 C、 D、9. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A、 B、 C、 D、9. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
 A、 B、 C、 D、10. 小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有一个根是x=-1 D、有两个相等的实数根
A、 B、 C、 D、10. 小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有一个根是x=-1 D、有两个相等的实数根二、填空题
-
11. 若最简二次根式 与 是同类根式,则 .12. 在 中,若 ,则 的度数是 .
13. 在一个不透明的袋子中只装有n个白球和2个红球,这些球除颜色外其他均相同.如果从袋子中随机摸出一个球,摸到红球的概率是 ,那么n的值为.14. 设 、 是方程 的两个实数根,则 的值为 .15. 如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .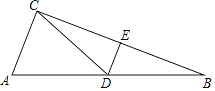
三、解答题
-
16. 计算(1)、2sin30°-tan60°+tan45°;(2)、 tan245°+sin230°-3cos230°17.(1)、用配方法解方程: ;(2)、用公式法解方程: .18. 如图,在 中, , 为 上一点, , .
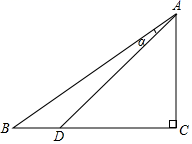 (1)、求 的长;(2)、求 的值.19. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆 人次,进馆人次逐月增加,到第三个月末累计进馆 人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过 人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.20. 我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点 处垂直海面发射,当火箭到达点 处时,海岸边 处的雷达站测得点 到点 的距离为8千米,仰角为30°.火箭继续直线上升到达点 处,此时海岸边 处的雷达测得 处的仰角增加15°,求此时火箭所在点 处与发射站点 处的距离.(结果精确到0.1千米)(参考数据: , )
(1)、求 的长;(2)、求 的值.19. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆 人次,进馆人次逐月增加,到第三个月末累计进馆 人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过 人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.20. 我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点 处垂直海面发射,当火箭到达点 处时,海岸边 处的雷达站测得点 到点 的距离为8千米,仰角为30°.火箭继续直线上升到达点 处,此时海岸边 处的雷达测得 处的仰角增加15°,求此时火箭所在点 处与发射站点 处的距离.(结果精确到0.1千米)(参考数据: , )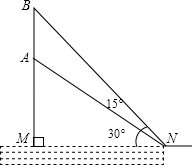 21. 有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
21. 有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.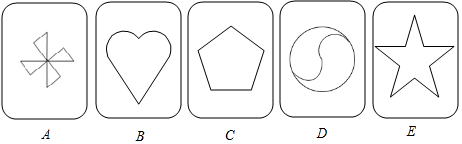 (1)、从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为.(2)、若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.22. 如图,
(1)、从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为.(2)、若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.22. 如图, (1)、某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO= ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB=°,AB= .(2)、请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6 ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.23. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
(1)、某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO= ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB=°,AB= .(2)、请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6 ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.23. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明) (1)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(2)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,BD=4,则DE的长为 .
(1)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(2)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,BD=4,则DE的长为 .