河南省信阳市浉河区2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-12-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程是一元二次方程的是（）

A、 $x (x - 1) = x^{2}$ B、x²=0 C、x²-2y=1 D、 $x = \frac{1}{x} - 1$

查看试题解析
3. 二次函数y＝（x﹣4）²+2图象的顶点坐标是（）

A、（﹣4，2） B、（4，﹣2） C、（4，2） D、（﹣4，﹣2）

查看试题解析
4. 关于x的一元二次方程x²﹣2x﹣m＝0有实根，则m的值可能是（）

A、 ﹣4 B、﹣3 C、﹣2 D、﹣1

查看试题解析
5. 如图，在⊙O，点A，B，C在⊙O上，若∠OAB＝54°，则∠C（）

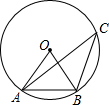A、54° B、27° C、36° D、46°

查看试题解析
6. 一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同.搅匀后任意摸出一个球，是黄球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{10}$ C、 $\frac{1}{5}$ D、 $\frac{7}{10}$

查看试题解析
7. 天虹商场一月份鞋帽专柜的营业额为100万元，三月份鞋帽专柜的营业额为150万元.设一到三月每月平均增长率为x，则下列方程正确的是（）

A、100（1+2x）＝150 B、100（1+x）²＝150 C、100（1+x）+100（1+x）²＝150 D、100+100（1+x）+100（1+x）²＝150

查看试题解析
8. 如图，在同一平面直角坐标系中，一次函数y₁＝kx+b（k、b是常数，且k≠0）与反比例函数y₂＝ $\frac{c}{x}$ （c是常数，且c≠0）的图象相交于A（﹣3，﹣2），B（2，m）两点，则不等式y₁＞y₂的解集是（）

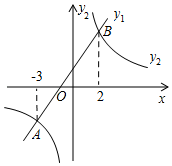A、﹣3＜x＜2 B、x＜﹣3或x＞2 C、﹣3＜x＜0或x＞2 D、0＜x＜2

查看试题解析
9. 如图是二次函数y＝ax²+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），说法：①abc＜0；②2a﹣b＝0；③﹣a+c＜0；④若（﹣5，y₁）、（ $\frac{5}{2}$ ，y₂）是抛物线上两点，则y₁＞y₂ ，其中说法正确的有（）个.

A、1 B、2 C、3 D、4

查看试题解析
10. 在平面直角坐标系中，若干个半径为1的单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，向右沿这条曲线做上下起伏运动（如图），点P在直线上运动的速度为每1个单位长度.点P在弧线上运动的速度为每秒 $\frac{π}{3}$ 个单位长度，则2019秒时，点P的坐标是（）

A、 $(\frac{2019}{2} ， \frac{\sqrt{3}}{2})$ B、 $(\frac{2019}{2} ， - \frac{\sqrt{3}}{2})$ C、 $(2019 ， \sqrt{3})$ D、 $(2019 ， - \sqrt{3})$

查看试题解析

二、填空题

11. 方程 $x^{2} = - 4 x$ 的根是.

查看试题解析
12. 如图，将 $Δ A B C$ 绕点 $A$ 逆时针旋转 $140^{\circ}$ ，得到 $Δ A D E$ ，这时点 $B ， C ， D$ 恰好在同一直线上，则 $∠ B$ 的度数为.

查看试题解析
13. 如图，点B是双曲线y＝ $\frac{k}{x}$ （k≠0）上的一点，点A在x轴上，且AB＝2，OB⊥AB，若∠BAO＝60°，则k＝.

查看试题解析
14. 如图，在边长为2的正方形ABCD中，以点D为圆心，AD长为半径画 $\overset{⌢}{AC}$ ，再以BC为直径画半圆，若阴影部分①的面积为S₁ ，阴影部分②的面积为S₂ ，则图中S₁﹣S₂的值为.（结果保留π）

查看试题解析
15. 如图，在▱ABCD中，AB＝6，BC＝6 $\sqrt{3}$ ，∠D＝30°，点E是AB边的中点，点F是BC边上一动点，将△BEF移沿直线EF折叠，得到△GEF ，当FG∥AC时，BF的长为．

查看试题解析

三、解答题

16. 解下列方程：

(1)、x²﹣2x﹣2=0；

(2)、（x﹣1）（x﹣3）=8.

查看试题解析
17. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别是A（﹣4，1），B（﹣1，2），C（﹣2，4）.

（ 1 ）将△ABC向右平移4个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点B₁的坐标；

（ 2 ）△A₂B₂C₂和△A₁B₁C₁关于原点O中心对称，请画出△A₂B₂C₂ ，并写出点C₂的坐标；

（ 3 ）连接点A和点B₂ ，点B和点A₂ ，得到四边形AB₂A₂B，试判断四边形AB₂A₂B的形状（无须说明理由）.

查看试题解析
18. 图①是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字1，2，3，4，图②是一个正六边形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）的数字之和是几，就从图②中的A点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法跳动．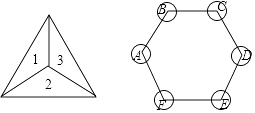

(1)、随机掷一次骰子，则棋子跳动到点C处的概率是

(2)、随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点C处的概率．

查看试题解析
19. 如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP.

(1)、求证：△BOQ≌△POQ；

(2)、若直径AB的长为12.
①当PE＝时，四边形BOPQ为正方形；

②当PE＝时，四边形AEOP为菱形.

查看试题解析

20. 参照学习函数的过程方法，探究函数

y = \frac{x - 2}{x} (x \neq 0)

的图象与性质，因为

y = \frac{x - 2}{x} = 1 - \frac{2}{x}

，即

y = - \frac{2}{x} + 1

，所以我们对比函数

y = - \frac{2}{x}

来探究列表：

$x$	…	-4	-3	-2	-1	$- \frac{1}{2}$	$\frac{1}{2}$	1	2	3	4	…
$y = - \frac{2}{x}$	…	$\frac{1}{2}$	$\frac{2}{3}$	1	2	4	-4	-2	-1	$- \frac{2}{3}$	$- \frac{1}{2}$	…
$y = \frac{x - 2}{x}$	…	$\frac{3}{2}$	$\frac{5}{3}$	2	3	5	-3	-2	0	$\frac{1}{3}$	$\frac{1}{2}$	…

描点：在平面直角坐标系中以自变量 $x$ 的取值为横坐标，以 $y = \frac{x - 2}{x}$ 相应的函数值为纵坐标，描出相应的点如图所示：

(1)、请把

y

轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；

(2)、观察图象并分析表格，回答下列问题：

①当 $x < 0$ 时， $y$ 随 $x$ 的增大而；（“增大”或“减小”）

② $y = \frac{x - 2}{x}$ 的图象是由 $y = - \frac{2}{x}$ 的图象向平移个单位而得到的；

③图象关于点中心对称.（填点的坐标）

(3)、函数

y = \frac{x - 2}{x}

与直线

y = - 2 x + 1

交于点

A

，

B

，求

Δ A O B

的面积.

查看试题解析

21. 某水果商场经销一种高档水果，原价每千克50元，连续两次降价后每千克32元，若每每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元？

查看试题解析
22. 在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线.

(1)、如图a，连接OC，请直接写出∠OCE和∠OAC的数量关系：；

(2)、点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N.
①如图b，猜想并证明线段OM和线段ON之间的数量关系；

②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度(用含m的代数式表示).

查看试题解析
23. 如图，若b是正数.直线l：y＝b与y轴交于点A，直线a：y＝x﹣b与y轴交于点B；抛物线L：y＝﹣x²+bx的顶点为C，且L与x轴右交点为D.

(1)、若AB＝6，求b的值，并求此时L的对称轴与a的交点坐标；

(2)、当点C在l下方时，求点C与l距离的最大值；

(3)、设x₀≠0，点（x₀ ， y₁），（x₀ ， y₂），（x₀ ， y₃）分别在l，a和L上，且y₃是y₁ ， y₂的平均数，求点（x₀ ， 0）与点D间的距离；

(4)、在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b＝2019和b＝2019.5时“美点”的个数.

查看试题解析