河南省新乡市辉县市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-12-15 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\frac{1}{\sqrt{1 - 2 x}}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x < \frac{1}{2}$ B、 $x < 2$ C、 $x \leq \frac{1}{2}$ D、 $x \geq 0$

查看试题解析
2. 方程 $x (x - 4) + x - 4 = 0$ 的解是（）

A、4 B、-4 C、-1 D、4或-1

查看试题解析
3. 如图，将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下，使木桩向上运动，已知楔子斜面的倾斜角为20°，若楔子沿水平方向前移8cm（如箭头所示），则木桩上升了（）

A、8tan20° B、 C、8sin20° D、8cos20°

查看试题解析
4. 如图，△ABC中，D是AB的中点，DE∥BC ，连接BE ．若AE=6，DE=5，∠BEC=90°，则△BCE的周长是（）

A、12 B、24 C、36 D、48

查看试题解析
5. 抛物线 $y = x^{2} + 6 x + 7$ 可由抛物线 $y = x^{2}$ 如何平移得到的（）

A、先向左平移3个单位，再向下平移2个单位 B、先向左平移6个单位，再向上平移7个单位 C、先向上平移2个单位，再向左平移3个单位 D、先回右平移3个单位，再向上平移2个单位

查看试题解析
6. 如图，以点O为位似中心，将△ABC放大得到△DEF，若AD＝OA，则△ABC与△DEF 的面积之比为（）

A、1：2 B、1：4 C、1：5 D、1：6

查看试题解析
7. 二次函数 $y = x^{2} - a x + b$ 的图象如图所示，对称轴为直线 $x = 2$ ，下列结论不正确的是（）

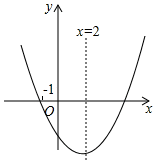A、 $a = 4$ B、当 $b = - 4$ 时，顶点的坐标为 $(2 ， - 8)$ C、当 $x = - 1$ 时， $b > - 5$ D、当 $x > 3$ 时，y随x的增大而增大

查看试题解析
8. 如图所示，矩形纸片ABCD中，AD=6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（）

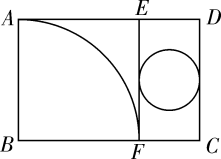A、3.5cm B、4cm C、4.5cm D、5cm

查看试题解析
9.
如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（　　）

A、 $\frac{1}{3}$ B、2 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
10. 如图，在 $R t Δ A B C$ 中，点 $D$ 为 $A C$ 边中点，动点 $P$ 从点 $D$ 出发，沿着 $D \to A \to B$ 的路径以每秒1个单位长度的速度运动到 $B$ 点，在此过程中线段 $C P$ 的长度 $y$ 随着运动时间 $x$ 的函数关系如图2所示，则 $B C$ 的长为（）

A、 $\frac{13 \sqrt{2}}{3}$ B、 $4 \sqrt{3}$ C、 $\frac{4 \sqrt{55}}{11}$ D、 $\frac{14 \sqrt{5}}{3}$

查看试题解析

二、填空题

11. 计算 $\sqrt{27} - 6 \sqrt{\frac{1}{3}}$ 的结果是.

查看试题解析
12. 抛物线 $y = (k + 1) x^{2} + k^{2} - 9$ 开口向下，且经过原点，则 $k =$ .

查看试题解析
13. 在一个不透明的袋子中有1个红球和3个白球，这些球除颜色外都相同，在袋子中再放入 $x$ 个白球后，从袋子中随机摸出1个球，记录下颜色后放回袋子中并搅匀，经大量试验，发现摸到白球的频率稳定在0.95左右，则 $x =$ .

查看试题解析
14. 如图，四边形ABCD是菱形，∠A＝60°，AB＝2，扇形EBF的半径为2，圆心角为60°，则图中阴影部分的面积是．

查看试题解析
15. 矩形ABCD中，AB=6，BC=8.点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC，若△APD是等腰三角形，则PE的长为数.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{4}{x + 3} - 1) \div \frac{x^{2} - 2 x + 1}{2 x + 6}$ ，其中 $x = 2 \cos 30 ° + \tan 45 °$ .

查看试题解析
17. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
18. 如图，AB是⊙O的弦，过点O作OC⊥OA，OC交于AB于P，且CP=CB。

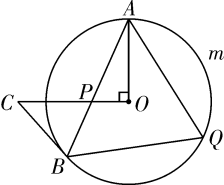(1)、求证：BC是⊙O的切线；

(2)、已知∠BAO=25°，点Q是弧AmB上的一点。
①求∠AQB的度数；

②若OA=18，求弧AmB的长。

查看试题解析
19. 某品牌太阳能热水器的实物图和横断面示意图如图所示．已知真空集热管DE与支架CB所在直线相交于点O，且 $O B = O E$ ；支架BC与水平线AD垂直． $A C = 40 cm$ ， $∠ A D E = 30 °$ ， $D E = 190 cm$ ，另一支架AB与水平线夹角 $∠ B A D = 65 °$ ，求OB的长度（结果精确到1cm；温馨提示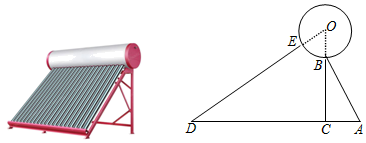： $sin 65 ° \approx 0.91$ ， $cos 65 ° \approx 0.42$ ， $tan 65 ° \approx 2.14$ ）

查看试题解析

20. 为了庆祝中华人民共和国成立70周年，某市决定开展“我和祖国共成长”主题演讲比赛，某中学将参加本校选拔赛的40名选手的成绩(满分为100分，得分为正整数且无满分，最低为75分)分成五组，并绘制了下列不完整的统计图表.

分数段	频数	频率
74.5～79.5	2	0.05
79.5～84.5	m	0.2
84.5～89.5	12	0.3
89.5～94.5	14	n
94.5～99.5	4	0.1

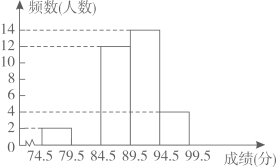(1)、表中m＝， n＝；

(2)、请在图中补全频数直方图；

(3)、甲同学的比赛成绩是40位参赛选手成绩的中位数，据此推测他的成绩落在分数段内；

(4)、选拔赛中，成绩在94.5分以上的选手，男生和女生各占一半，学校从中随机确定2名选手参加全市决赛，请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看试题解析

21. 某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克，规定销售单价不低于成本，又不高于成本的两倍.经过市场调查发现，某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示：

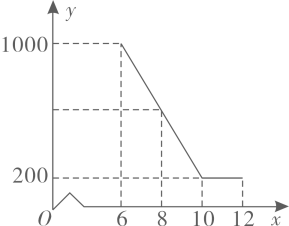(1)、求y与x的函数解析式(也称关系式)；

(2)、求这一天销售西瓜获得的利润的最大值.

查看试题解析
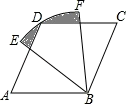
22.

(1)、某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO= $3 \sqrt{3}$ ，BO：CO=1：3，求AB的长.

经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）.

请回答：∠ADB=°，AB=.

(2)、请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO= $3 \sqrt{3}$ ，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长.

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + 3$ 与x轴分别交于 $A (- 3，0)$ ， $B (1，0)$ 两点，与y轴交于点C.

(1)、求抛物线的表达式及顶点D的坐标；

(2)、点F是线段AD上一个动点.
①如图1，设 $k = \frac{A F}{A D}$ ，当k为何值时， $C F = \frac{1}{2} A D$ .

②如图2，以A，F，O为顶点的三角形是否与 $Δ A B C$ 相似？若相似，求出点F的坐标；若不相似，请说明理由.

查看试题解析