河南省平顶山市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-12-15 类型：期末考试

进入出卷网下载

一、单选题

1. 用配方法解方程 $x^{2} + 6 x - 4 = 0$ ，下列变形正确的是（）

A、 ${(x + 3)}^{2} = 5$ B、 ${(x + 3)}^{2} = - 5$ C、 ${(x - 3)}^{2} = - 13$ D、 ${(x + 3)}^{2} = 13$

查看试题解析
2. 如图是某零件的模型，则它的左视图为（）

A、 B、 C、 D、

查看试题解析
3. 已知矩形ABCD，下列结论错误的是（）

A、AB＝DC B、AC＝BD C、AC⊥BD D、∠A+∠C＝180°

查看试题解析
4. 已知关于x的一元二次方程kx²－2x＋1＝0有实数根，则k的取值范围是（）.

A、k<1 B、k≤1 C、k≤1且k≠0 D、k<1且k≠0

查看试题解析
5. 某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A、50（1+x²）=196 B、50+50（1+x²）=196 C、50+50（1+x）+50（1+x）²=196 D、50+50（1+x）+50（1+2x）=196

查看试题解析
6. 如图，太阳在A时测得某树（垂直于地面）的影长ED＝2米，B时又测得该树的影长CD＝8米，若两次日照的光线PE⊥PC交于点P，则树的高度为PD为（）

A、3米 B、4米 C、4.2米 D、4.8米

查看试题解析
7. 有一张矩形纸片ABCD，AB=2.5，AD=1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F（如图），则CF的长为（）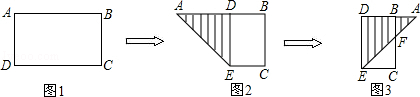

A、1 $\frac{1}{3}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的周长之比为1：2，点C的坐标为（﹣2，0），若点B的坐标为（﹣5，1），则点D的坐标为（）

A、（4，﹣2） B、（6，﹣2） C、（8，﹣2） D、（10，﹣2）

查看试题解析
9. 已知k₁＜0＜k₂ ，则函数y=k₁x和 $y = \frac{k_{2}}{x}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，已知▱ABCD中，∠DBC＝45°，DE⊥BC于E，BF⊥CD于F，DE、BF相交于H，BF、AD的延长线相交于G，下面结论：①DB＝ $\sqrt{2}$ BE；②∠A＝∠BHE；③AB＝BH；④△BHD∽△BDG.其中正确的结论是（）

A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析

二、填空题

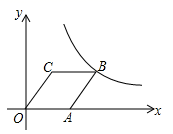
11. 若a、b、c、d满足 $\frac{a}{b}$ = $\frac{c}{d}$ = $\frac{3}{4}$ ，则 $\frac{a + c}{b + d}$ = ．

查看试题解析
12. 在一个不透明的布袋中，有红球、白球共30个，除颜色外其它完全相同，小明通过多次摸球试验后发现，其中摸到红球的频率稳定在40%，则随机从口袋中摸出一个是红球的概率是.

查看试题解析
13. 已知2是关于 $x$ 的一元二次方程 $x^{2} + 4 x - p = 0$ 的一个根，则该方程的另一个根是．

查看试题解析
14. 如图，菱形 $O A B C$ 的顶点C的坐标为 $(3 ， 4)$ ，顶点A在x轴的正半轴上.反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过顶点B，则k的值为.

查看试题解析
15. 如图，四边形ABCD是边长为4的正方形，若AF＝3，E为AB上一个动点，把△AEF沿着EF折叠，得到△PEF，若△BPE为直角三角形，则BP的长度为.

查看试题解析

三、解答题

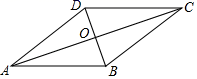
16. 解方程

(1)、x²﹣4x+2＝0

(2)、（x﹣3）²＝2x﹣6

查看试题解析
17. 2020年元且，某商场为促销举办抽奖活动.规则如下：在一个不透明的纸盒里，装有2个红球和2个黑球，这些球除颜色外都相同.顾客每次摸出1个球，若摸到红球，则获得一份奖品；若摸到黑球，则没有奖品.

(1)、如果张大妈只有一次摸球机会，那么张大妈获得奖品的概率是.

(2)、如果张大妈有两次摸球机会（摸出后不放回），请用“树状图”或“列表”的方法，求张大妈获得两份奖品的概率.

查看试题解析
18. 如图，在四边形ABCD中，AB∥CD，AB＝AD，对角线AC、BD交于点O，AC平分∠BAD.求证：四边形ABCD为菱形.

查看试题解析
19. 如图，在阳光下的电线杆AB落在地上的影子BD长3米，落在墙上的影子CD的高为2米，同一时刻，竖起一根1米高的竹竿MN，其影长MF为1.5米，求电线杆的高度.

查看试题解析

20. 一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

售价x（元/千克）	…	50	60	70	80	…
销售量y（千克）	…	100	90	80	70	…

(1)、求y与x的函数关系式；

(2)、该批发商若想获得4000元的利润，应将售价定为多少元？

查看试题解析

21. 如图，一次函数y=﹣x+2的图象与反比例函数y=﹣ $\frac{3}{x}$ 的图象交于A、B两点，与x轴交于D点，且C、D两点关于y轴对称．

(1)、求A、B两点的坐标；

(2)、求△ABC的面积．

查看试题解析
22. 如图，在△ABC中，∠C＝90°，AC＝6cm，BC＝8m，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从点C出发沿CB边向点B以2cm/s的速度移动，当其中一点到达终点时，另一点也随之停止运动.

(1)、如果点P，Q同时出发，经过几秒钟时△PCQ的面积为8cm²？

(2)、如果点P，Q同时出发，经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似？

查看试题解析
23. 已知，在△ABC中，∠BAC＝90°，∠ABC＝45°，点D为直线BC上一动点（点D不与点B、C重合），以AD为边做正方形ADEF，连接CF.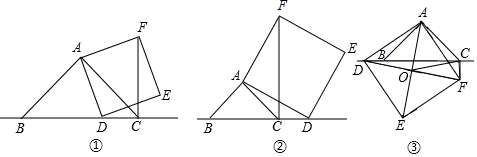

(1)、如图①，当点D在线段BC上时，直接写出线段CF、BC、CD之间的数量关系.

(2)、如图②，当点D在线段BC的延长线上时，其他件不变，则（1）中的三条线段之间的数量关系还成立吗？如成立，请予以证明，如不成立，请说明理由；

(3)、如图③，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC两侧，其他条件不变；若正方形ADEF的边长为4，对角线AE、DF相交于点O，连接OC，请直接写出OC的长度.

查看试题解析