河南省南阳市内乡县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-12-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，为最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{2}$ C、 $\sqrt{4}$ D、 $\sqrt{12}$

查看试题解析
2. 方程5x²﹣2＝﹣3x的二次项系数、一次项系数、常数项分别是（）

A、5、3、﹣2 B、5、﹣3、﹣2 C、5、3、2 D、5、﹣3、2

查看试题解析
3. 若△ABC∽△ADE，若AB=6，AC=4，AD=3，则AE的长是（）

A、1 B、2 C、1.5 D、3

查看试题解析
4. 在70周年国庆阅兵式上有两辆阅兵车的车牌号如图所示（每辆阅兵车的车牌号含7位数字或字母），则“9”这个数字在这两辆车牌号中出现的概率为（）

A、 $\frac{3}{7}$ B、 $\frac{3}{14}$ C、 $\frac{3}{26}$ D、 $\frac{1}{12}$

查看试题解析
5. 一个小正方体沿着斜面 $A C$ 前进了10 米，横截面如图所示，已知 $A B = 2 B C ， ∠ A B C = 90 °$ ，此时小正方体上的点 $N$ 距离地面 $A B$ 的高度升高了（）

A、5米 B、 $2 \sqrt{5}$ 米 C、 $4 \sqrt{5}$ 米 D、 $\frac{10}{3}$ 米

查看试题解析
6. 如图，四边形ABCD内接于⊙O ，若它的一个外角∠DCE＝65°，∠ABC＝68°，则∠A的度数为（　　）.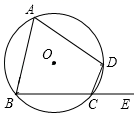

A、112° B、68° C、65° D、52°

查看试题解析
7. 已知a、b、c为常数，点P（a，c）在第二象限，则关于x的方程ax²+bx+c=0根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断

查看试题解析
8. 如图，在△ABC中，AB＝AC，D，E，F分别是边AB，AC，BC的中点，若CE＝2，四边形ADFE的周长为（）

A、2 B、4 C、6 D、8

查看试题解析
9. 二次函数y＝ax²＋bx＋c的图象如图所示，若点A(-2.2，y₁)，B(-3.2，y₂)是图象上的两点，则y₁与y₂的大小关系是（）.

A、y₁＜y₂ B、y₁＝y₂ C、y₁＞y₂ D、不能确定

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C = 10 c m$ ， $F$ 为 $A B$ 上一点， $A F = 2$ ，点 $E$ 从点 $A$ 出发，沿 $A C$ 方向以 $2 c m / s$ 的速度匀速运动，同时点 $D$ 由点 $B$ 出发，沿 $B A$ 方向以 $1 c m / s$ 的速度匀速运动，设运动时间为 $t (s) (0 < t < 5)$ ，连接 $D E$ 交 $C F$ 于点 $G$ ，若 $C G = 2 F G$ ，则 $t$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算： $\sqrt{7}$ × $\sqrt{14}$ =.

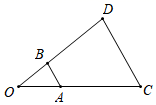
查看试题解析
12. 如图，以点O为位似中心，将 $Δ O A B$ 放大后得到 $Δ O C D$ ， $O A = 2 ， A C = 3$ ，则 $\frac{A B}{C D} =$ ．

查看试题解析
13. 用配方法解一元二次方程 $x^{2} + 4 x - 3 = 0$ ，配方后的方程为 ${(x + 2)}^{2} = n$ ，则n的值为.

查看试题解析
14. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉．在《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道 $A B = 1$ 尺（1尺＝10寸），则该圆材的直径为寸．

查看试题解析
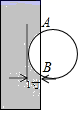15. 已知函数 $y = {\begin{array}{l} - x^{2} + 2 x (x > 0) \\ x (x \leq 0) \end{array}$ 的图象如图所示，若直线 $y = x + m$ 与该图象恰有两个不同的交点，则 $m$ 的取值范围为.

查看试题解析

三、解答题

16. 计算： ${(1 - π)}^{0} + | \sqrt{2} - \sqrt{3} | - \sqrt{12} + {(\frac{1}{\sqrt{2}})}^{- 1}$

查看试题解析
17. 有5张不透明的卡片，除正面上的图案不同外，其它均相同.将这5张卡片背面向上洗匀后放在桌面上.若从中随机抽取1张卡片后不放回，再随机抽取1张，请用画树状图或列表的方法，求两次所抽取的卡片恰好都是轴对称图形的概率.

查看试题解析
18. 安顺市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量 $y$ （千克）与每千克降价 $x$ （元） $(0 < x < 20)$ 之间满足一次函数关系，其图象如图所示：

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、商贸公司要想获利2090元，则这种干果每千克应降价多少元？

查看试题解析
19. 如图， $⊙ O$ 中，弦 $A B$ 与 $C D$ 相交于点 $E$ ， $A B = C D$ ，连接 $A D 、 B C$ .求证： $A E = C E$ .

查看试题解析
20. 如图，学校教学楼上悬挂一块长为 $3 m$ 的标语牌，即 $C D = 3 m$ .数学活动课上，小明和小红要测量标语牌的底部点 $D$ 到地面的距离.测角仪支架高 $A E = B F = 1.2 m$ ，小明在 $E$ 处测得标语牌底部点 $D$ 的仰角为 $31 °$ ，小红在 $F$ 处测得标语牌顶部点 $C$ 的仰角为 $45 °$ ， $A B = 5 m$ ，依据他们测量的数据能否求出标语牌底部点 $D$ 到地面的距离 $D H$ 的长？若能，请计算；若不能，请说明理由（图中点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ ， $H$ 在同一平面内）
（参考数据： $\tan 31 ° \approx 0.60$ ， $\sin 31 ° \approx 0.52$ ， $\cos 31 ° \approx 0.86)$

查看试题解析
21. 如图，在等腰 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 6$ ， $D$ 是 $A C$ 上一点，若 $\tan ∠ D B A = \frac{1}{5}$ .

(1)、求 $A D$ 的长；

(2)、求 $\sin ∠ D B C$ 的值.

查看试题解析
22. 如图，在正方形ABCD中，点M、N分别在AB、BC上，AB=4，AM=1，BN= $\frac{3}{4}$ .

(1)、求证：ΔADM∽ΔBMN；

(2)、求∠DMN的度数.

查看试题解析
23. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ 和点 $C (0 ， 4)$ ，交 $x$ 轴正半轴于点 $B$ ，连接 $A C$ ，点 $E$ 是线段 $O B$ 上动点（不与点 $O ， B$ 重合），以 $O E$ 为边在 $x$ 轴上方作正方形 $O E F G$ ，接 $F B$ ，将线段 $F B$ 绕点 $F$ 逆时针旋转90°，得到线段 $F P$ ，过点 $P$ 作 $P H / / y$ 轴， $P H$ 交抛物线于点 $H$ ，设点 $E (a ， 0)$ .

(1)、求抛物线的解析式；

(2)、若 $Δ A O C$ 与 $Δ F E B$ 相似求 $a$ 的值；

(3)、当 $P H = 2$ 时，求点 $P$ 的坐标.

查看试题解析