河南省洛阳市嵩县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-12-15 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\frac{\sqrt{x + 1}}{x}$ 有意义，则 $x$ 的取值范围是（）

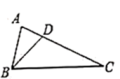
A、 $x \geq - 1$ B、 $x > - 1$ 且 $x \neq 0$ C、 $x \neq 0$ D、 $x \geq - 1$ 且 $x \neq 0$

查看试题解析
2. 一元二次方程x²+4x＝﹣3用配方法变形正确的是（）

A、（x﹣2） $^{2}$ ＝1 B、（x+2） $^{2}$ ＝1 C、（x﹣2） $^{2}$ ＝﹣1 D、（x+2） $^{2}$ ＝﹣1

查看试题解析
3. 若两个最简二次根式 $\sqrt{n^{2} - 2 n}$ 和 $\sqrt{n + 4}$ 是同类二次根式，则n的值是（）

A、﹣1 B、4或﹣1 C、1或﹣4 D、4

查看试题解析
4. 如图， $Δ A B C$ 中， $∠ A B D = ∠ C$ ，若 $A B = 4$ ， $A D = 2$ ，则 $C D$ 边的长是（）

A、2 B、4 C、6 D、8

查看试题解析
5. 如图，将△ABC的三个顶点坐标的横坐标都乘以-1，并保持纵坐标不交，则所得图形与原图形的关系是（）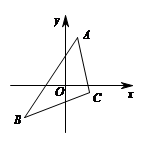

A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位

查看试题解析
6. 在△ABC中，tanC＝ $\frac{\sqrt{3}}{3}$ ，cosA＝ $\frac{\sqrt{2}}{2}$ ，则∠B＝（）

A、60° B、90° C、105° D、135°

查看试题解析
7. 如图，已知△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的 $\frac{4}{9}$ ，则AO：AD的值为（）

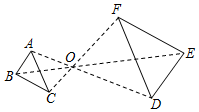A、2：3 B、2：5 C、4：9 D、4：13

查看试题解析
8. 计算 $(\sqrt{7} + \sqrt{3}) (\sqrt{7} - \sqrt{3}) - {(2 \sqrt{3} + 1)}^{2} + \frac{\sqrt{48} - \sqrt{27}}{\sqrt{3}}$ 的结果为（）

A、8﹣4 $\sqrt{3}$ B、﹣8﹣4 $\sqrt{3}$ C、﹣8+4 $\sqrt{3}$ D、8+4 $\sqrt{3}$

查看试题解析
9. 如图，四边形ABCD中，∠A＝90°，AB＝12，AD＝5，点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的可能为（）

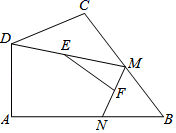A、2 B、5 C、7 D、9

查看试题解析
10. 如图，在正方形ABCD中，H是对角线BD的中点，延长DC至E，使得DE=DB，连接BE，作DF⊥BE交BC于点G，交BE于点F，连接CH、FH，下列结论：（1）HC=HF；（2）DG=2EF；（3）BE·DF=2CD²；（4）S_△_BDE=4S_△_DFH；（5）HF∥DE，正确的个数是（）

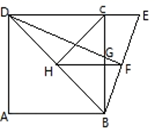A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. $2 \sin 45^{\circ} + 2 \cos 60^{\circ} - \sqrt{3} \tan 60^{\circ} =$ .

查看试题解析
12. 已知实数a、b、c在数轴上的位置如图所示，化简 $\sqrt{{(a + c)}^{2}} - | b + c |$ =.

查看试题解析
13. 一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小文在袋中放入3个白球(每个球除颜色外其余都与红球相同).摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.7左右，则袋中红球约有个.

查看试题解析
14. 如图，在平行四边形ABCD中，AE：BE＝2：1，F是AD的中点，射线EF与AC交于点G，与CD的延长线交于点P，则 $\frac{A G}{G C}$ 的值为.

查看试题解析
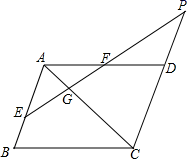15. 如图，△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，CD是△ABC的中线，E是AC上一动点，将△AED沿ED折叠，点A落在点F处，EF线段CD交于点G，若△CEG是直角三角形，则CE＝.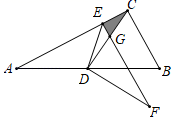

查看试题解析

三、解答题

16. 已知a＝ $\frac{1}{\sqrt{5} - 2}$ ，b＝ $\frac{1}{\sqrt{5} + 2}$ ，求 $\sqrt{a^{2} + b^{2} - a b + 8}$ .

查看试题解析
17. 如图，△ABC在坐标平面内，三个顶点的坐标分别为A（0，4），B（2，2），C（4，6）（正方形网格中，每个小正方形的边长为1）

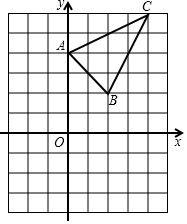
（ 1 ）画出△ABC向下平移5个单位得到的△A₁B₁C₁ ，并写出点B₁的坐标；

（ 2 ）以点O为位似中心，在第三象限画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为1：2，直接写出点C₂的坐标和△A₂B₂C₂的面积.

查看试题解析
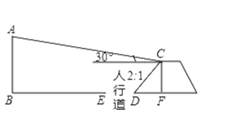
18. 2018年非洲猪瘟疫情暴发后，今年猪肉价格不断走高，引起了民众与政府的高度关注，据统计：今年7月20日猪肉价格比今年年初上涨了60%，某市民今年7月20日在某超市购买1千克猪肉花了80元钱．

(1)、问：今年年初猪肉的价格为每千克多少元？

(2)、某超市将进货价为每千克65元的猪肉，按7月20日价格出售，平均一天能销售出100千克，经调查表明：猪肉的售价每千克下降1元，其日销售量就增加10千克，超市为了实现销售猪内每天有1560元的利润，并且可能让顾客得到实惠，猪肉的售价应该下降多少元？

查看试题解析
19. 如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．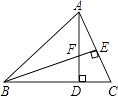

(1)、求证：△ACD∽△BFD；

(2)、当tan∠ABD=1，AC=3时，求BF的长．

查看试题解析
20. 城市规划期间，欲拆除一电线杆AB，已知距电线杆AB水平距离14m的D处有一大坝，背水坡CD的坡度i=2：1，坝高CF为2m，在坝顶C处测得杆顶A的仰角为30°，D、E之间是宽为2m的人行道.
试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？请说明理由（在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域.）（ $\sqrt{3}$ ≈1.732， $\sqrt{2}$ ≈1.414）

查看试题解析
21. 为了解某县建档立卡贫困户对精准扶贫政策落实的满意度，现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查（把调查结果分为四个等级：A级：非常满意；B级：满意；C级：基本满意；D级：不满意），并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题：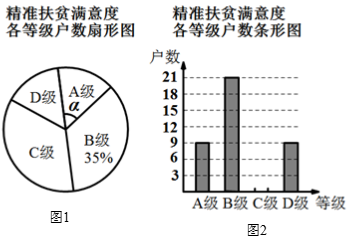

(1)、本次抽样调查测试的建档立卡贫困户的总户数.

(2)、图1中，求∠α的度数，并把图2条形统计图补充完整.

(3)、某县建档立卡贫困户有10000户，如果全部参加这次满意度调查，请估计非常满意的人数约为多少户？

(4)、调查人员想从5户建档立卡贫困户（分别记为 $a ， b ， c ， d ， e$ ）中随机选取两户，调查他们对精准扶贫政策落实的满意度，请用列表或画树状图的方法求出选中贫困户 $e$ 的概率.

查看试题解析
22.

(1)、如图1，已知∠ACB=∠DCE=90°，AC=BC=6，CD=CE，AE=3，∠CAE=45°，求AD的长.

(2)、如图2，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°，AC=3，AE=8，求AD的长.

查看试题解析
23. 如图，P是平面直角坐标系中第四象限内一点，过点P作PA⊥x轴于点A，以AP为斜边在右侧作等腰Rt△APQ，已知直角顶点Q的纵坐标为﹣2，连结OQ交AP于B，BQ＝2OB.

(1)、求点P的坐标；

(2)、连结OP，求△OPQ的面积与△OAQ的面积之比.

查看试题解析